# Proposal for mitigation against balancing attacks to LMD GHOST One key way in which eth2's fork choice differs from that of eth1, as well as "chain-based" PoS algorithms (eg. older algorithms like Peercoin and NXT, but also newer ones like Tezos, Ouroboros...) is that in eth2, there are many messages affecting the "score" of a block arriving in parallel. ### Chain-based:  ### Committee-per-slot (as in eth2):  Chain-based algorithms are easier to prove liveness for (and indeed, in some cases liveness has been proven), because there is generally a single actor acting at one time, allowing them to act as a "coordinating bottleneck" getting everyone to agree on the same score. Here is a "strawman proof sketch" for liveness in chain-based algorithms. Suppose that: 1. There is exactly one actor (eg. a block proposer) who can participate in each slot. 2. Honest block proposers publish their block during the first half of the slot. 3. Network latency is bounded above by half a slot (so $\delta < \frac{1}{2}$, measuring time in slots). 4. An actor assigned to take action (eg. propose a block) during slot $N+1$ will act based only on information that they received before the end of slot $N$. 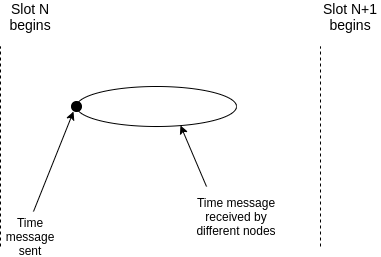We model the time during which nodes receive a message sent at time $t$ as a "cloud" in the interval $(t, t+\delta)$ (so far, this is just stating the standard academic presentation of a synchrony assumption). 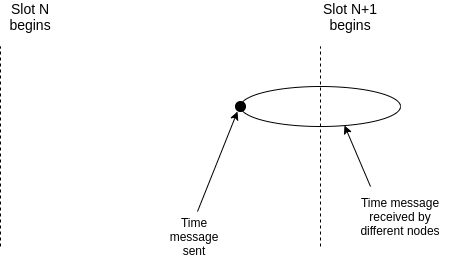Thus there are two cases: ### Agreement case  ### Disagreement case  Notice that the disagreement case happens only when the participant in slot N is dishonest. Hence, if the participant assigned to some given slot is honest, then either (i) at the end of that slot everyone agrees what the correct chain is, because they are calculating the fork choice based on the same information, or (ii) the attacker "used up" some saved participation rights from an even earlier slot in which they did not participate. Hence, a disruption can only continue if the attacker has at least one saved participation right per honest participant, ie. if the attacker is assigned to more slots than honest nodes (ie. the honest majority assumption is violated). Now, let's look at the "many parallel attestations" case. In the case where there are many parallel attestations that contribute to the score of a block, there is no single actor that creates a bottleneck in this way. Hence, an attacker could manipulate the network (plus strategically broadcast a few of their own validators) in such a way as to create a state of disagreement at the end of each slot about which messages count toward the fork choice, and therefore which of multiple chains is the winning chain. See [here](https://arxiv.org/pdf/2009.04987.pdf), particularly pages 4-5, for an exposition of this kind of attack. Note that this attack does depend on networking assumptions that are highly contrived in practice (the attacker having fine-grained control over latencies of individual validators), but nevertheless a protocol that is secure against such attacks is better than one that is not. ## Proposed solution The proposed solution is to introduce an explicit "synchronization bottleneck" gadget into the fork choice. In particular, we add the following rules: 1. Suppose that all of the attesters assigned to slot $N$ have collective total weight $W$ 2. A participant in slot $N+1$ only considers attestations valid if they arrived before the end of slot $N$ (from their point of view) 3. The _proposer_ in slot $N+1$ is expected to make a proposal immediately at the start of slot $N+1$. Their proposal implicitly chooses a particular chain. From the point of view of _attesters_ in slot N+1, if they see the proposal arriving before 1/3 of the way into a slot, they treat that proposal as equivalent to an attestation with weight $\frac{W}{4}$ (this score adjustment is valid only for slot $N+1$; after slot $N+1$ this score adjustment is reverted). 4. 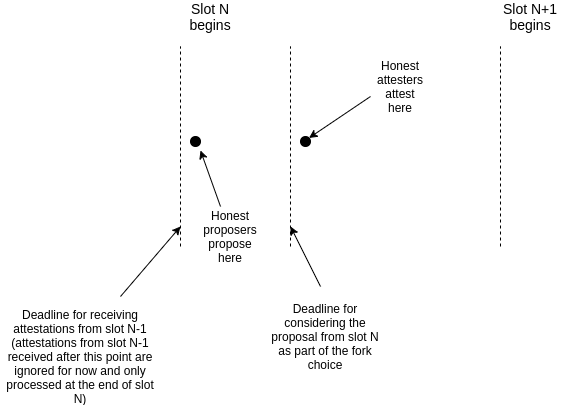Reduce the synchrony assumption to $\delta < \frac{1}{3}$  ### Analysis _(Note: for ease of analysis, we pretend that clocks are perfectly synchronous, and that any actual clock disparity is part of the network delay)_ At the end of slot $N$, all validators have received some set of attestations. If there is an attack going on (ie. there were $k\ge1$ malicious attesters that revealed attestations during slot $N$), the validators will likely disagree on the score of each block. But the range of their disagreement will be bounded-above by $k$. Suppose (without loss of generality) that there are two competing blocks, $A$ and $B$, and $A$ "wins" if $score(A) - score(B) \ge 0$ and otherwise $B$ wins. The range of disagreement in $score(A) - score(B)$ will be bounded above by $2k$ (ie. each validator's opinion on the value $score(A) - score(B)$ will be in some range $[z, z+2k]$ for a fixed $z$) Let $W_p$ be the weight of the proposer ($W_p = \frac{W}{4}$ in the exposition above). If the proposer is honest, they are guaranteed to follow two behaviors: 1. If they see that $score(A) - score(B) \ge 0$, they will propose a block on top of $A$; otherwise they will propose a block for $B$. 2. They will propose their block immediately, guaranteeing that all attesters see it before the deadline. Let $[z, z+2k]$ be the range of disagreement on $score(A) - score(B)$. We distinguish three cases: 1. $z < -2k$ 2. $-2k \le z < 0$ 3. $z \ge 0$ In case (1), the proposer wil vote for $B$, and so attesters will see adjusted scores in the range $[z-W_p, z+2k-W_p]$; this entire range is negative, and so there is full agreement on $B$. In case (3), the proposer will vote for $A$, and so attesters will see adjusted scores in the range $[z+W_p, z+2k+W_p]$; this entire range is positive, and so there is full agreement on $A$. In case (2), effectively the proposer decides. Depending on where in the range the proposer's own opinion falls, either the proposer favors $A$ or $B$. Hence, the range will be either (i) $[z-W_p, z+2k-W_p]$ or (ii) $[z+W_p, z+2k+W_p]$. Consider the case where $W_p \ge 2k$. Note that from the definition of case (2), $-2k \le z < 0$ In case (2.i), $z < 0$ and $2k - W_p \le 0$, so the upper end of the range $z+2k-W_p$ is negative, so the entire range is negative. In case (2.ii), $z > -2k$ and $W_p \ge 2k$, so $z + W_p > 0$, so the entire range is positive. Hence, there is full agreement on either $A$ or $B$, depending on the proposer's pick. Now, let's get back to the exposition, where $W_p = \frac{W}{4}$. To prevent the proposer synchronization bottleneck from working, the key premise in the above reasoning that $W_p \ge 2k$ must be broken; hence, there must be $>\frac{W}{4}$ attesters that reveal themselves during each slot. If the proposer synchronization bottleneck _works_ during any single slot, all honest attesters will vote in that direction, further pushing $score(A) - score(B)$ away from zero. To prevent one side or the other from winning at this point, the attacker must reveal enough attestations to counteract all honest validators during that slot (minus $\frac{1}{4}$ to counteract the loss of the proposer vote's efficacy at the end of the slot); this will take much more than $\frac{W}{4}$ attestations. Hence, maintaining a persistent liveness break requires at least $\frac{W}{4}$ malicious validators per slot, or $\ge \frac{1}{4}$ of validators to be dishonest.