# Safe Block Confirmation Rule [toc] We want to find out if a block $b$ is safe against reorgs under the following assumptions: - The adversary: - controls `< 50%` of stake - is willing to get $B$ stake slashed (not the amount slashed, but the sum of stake of validators who are slashed) - The network: - is synchronous with a maximum delay of $< \Delta = 4$ seconds ## Safe Block Rule We want to find out if block $b$ is safe. Let: - $t$ be the slot of block $b$ - $T$ be the current slot - $v(b)^i$ denote the LMD GHOST votes: - from committees in slots $[t, T]$, and - voting for blocks in the chain of $b$, and - in support of block at slot $i$ in the chain of $b$ - $W$ be the weight of the committee at each slot - $W_p$ be the weight of the proposer boost **Note:** $b$ is only ever a safe block if all ancestors of $b$ are also safe blocks. Checkpoint blocks have extra steps to determine their safety (discussed later). We only need to check the ancestors uptil the finalized head. The following calculations are for determining if block $b$ is safe under the assumption that all ancestors of $b$ are safe. **Note:** We are assuming that equivocating votes are deleted from the LMD weights. This is a proposed change to the protocol - currently the first seen vote is counted even when an equivocating vote is observed. | Description | Formula | |:---------------------------------------------- |:---------------- | | $A$: Actual votes in support of $b$ | $v(b)^t$ | | $C$: Committeed votes in the chain of $b$ | $v(b)^0$ | | $P$: Potential votes in the chain of $b$ | $(T-t+1) W$ | | $B$: Attacker's potentially equivocating votes | $B$ | In the worst case, votes that support: - the chain descending from $b$ are $A - B$ - any other competing chain are $P - C + W_p$ $b$ is safe if $A - B > P - C + W_p$, which reduces to: $v(b)^t + v(b)^0 - (T-t+1)W - W_p - B > 0$ ### Illustration of vote counting  $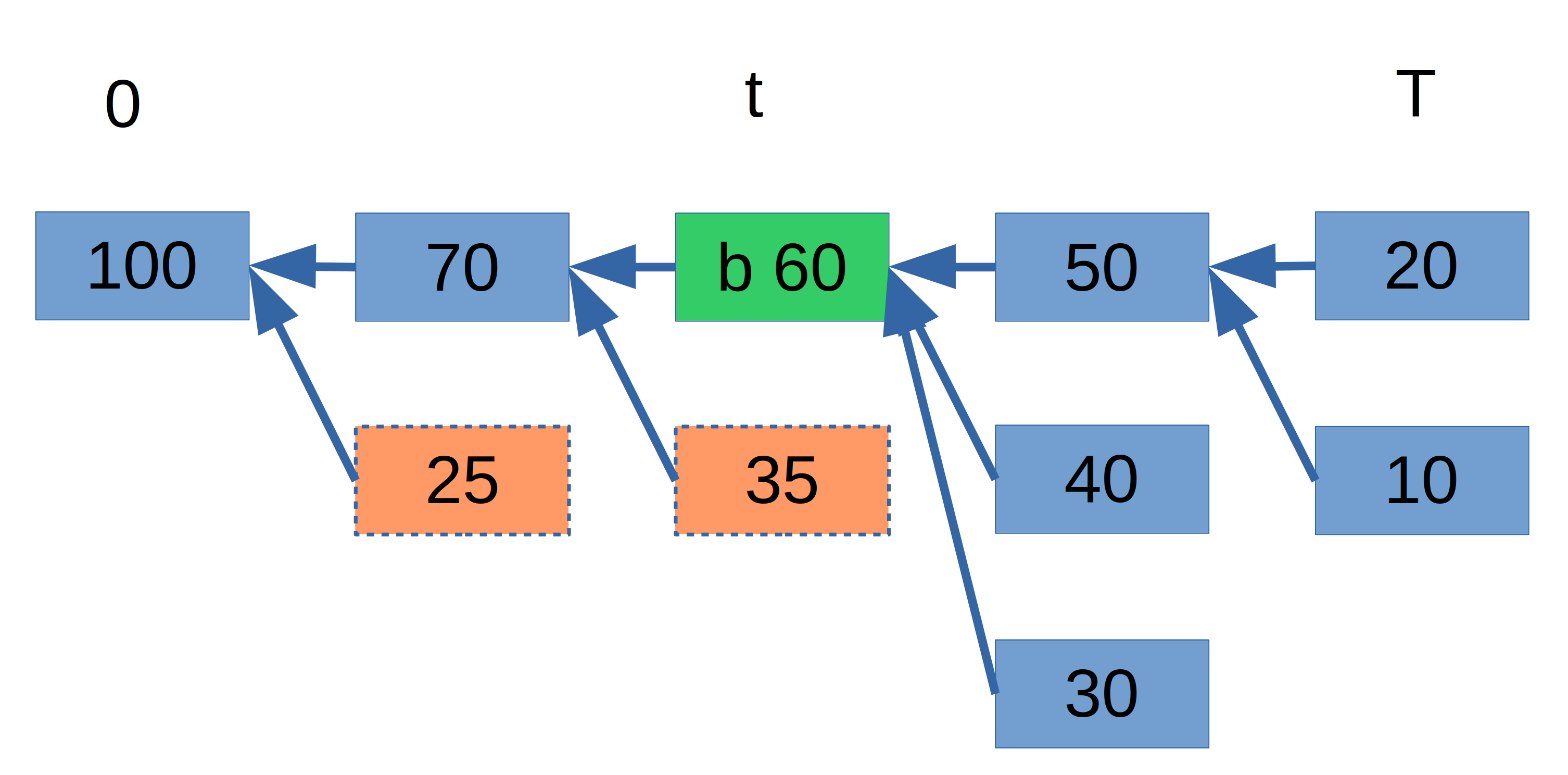v(b)^i$ counts all LMD GHOST votes from committees in slots $[t,T]$ made for a block at height $i$ that is in the chain of $b$. So that means a vote should be counted if it is either for a descendent of $b$, for $b$ itself, or for a *direct ancestor* of $b$. A vote that is in support of an ancestor, but for a chain that forks off the chain before $b$, is not in support for $b$'s chain and should thus not be counted. Example: * To evaluate $v(b)^0$, we sum $100+70+60+(50+40+30)+(20+10)=380$. The orange votes should not be counted (they are not in support of $b$). * $v(b)^t=60+(50+40+30)+(20+10)=190$ ### Guarantees - The safe head is always an ancestor of the latest head (tip of the fork choice rule) - Under the assumptions any block that is found to be a safe head will always remain an ancestor of the latest head, and always be a safe block - Any block proposed in time on top of a tip that is also a safe head will itself become a safe head ### Algorithm Clients use the protoarray algorithm ([description](https://github.com/protolambda/lmd-ghost#array-based-stateful-dag-proto_array), [Lighthouse source code](https://github.com/sigp/lighthouse/blob/b22ac95d7fe1734c5c204c1ed8adb3814e4a5deb/consensus/proto_array/src/proto_array.rs#L16-L46)). The protoarray weight of a block is the sum total of votes in support of that block. Let's break down the terms in the formula: - $- (T-t+1)W - W_p - B$ is easy to compute - $v(b)^t$ is the protoarray weight of block $b$ - $v(b)^0$ is not immediately available Let's look at what $v(b)^0$ computes: all the votes from committees in slots $\geq t$ that vote for any block in the chain of $b$. Among the honest committee members from slots $\geq t$, only those will vote for a block at slot $<t$ that do not see block $b$ at the time of their vote. The required latency for them to not see block at slot: - $t$ is `4 sec` - $t-1$ is `16 sec` - $t-k$ is `4 + 12*k sec` We can capture a large fraction of $v(b)^0$ in $v(b)^{t-k}$ assuming that the latency does not cross `4 + 12*k sec`. For simplicity of the algorithm, we can consider only $v(b)^{t-1}$. **QUESTION:** Is there a good way to get $v(b)^{t-1}$, which is the votes from committees in $[t,T]$ that vote directly for (i.e., have `attestation.data.beacon_block_root` set to) the parent of $b$? <!-- **TODO:** Broken - protoarray tracks all attestations, whereas we only need those from committees in slot $[t,T]$. --> <!-- $v(b)^{t-1}$ can be computed by subtracting the protoarray weights of all siblings of $b$ from the protoarray weight of the parent of $b$. **Note**: It is even easier to compute $v(b)^{t-1}$ if we add to the protoarray a `directweight` field, which only counts the direct head attestations to a block (instead of the cumulative votes in support). Then $v(b)^{t-1} = v(b)^{t} + \mathrm{directweight(parent(b))}$ --> So, we simplify the formula to: $v(b)^t + v(b)^{t-1} - (T-t+1)W - W_p - B > 0$ #### Timing considerations We want a guarantee that honest validators will vote according to the same view as ours. This means that we should not evaluate the safe head rule during the first 4s of any slot: During this time, we might see new attestations that do not have enough time to propagate through the network given the delay $\Delta$. In order to not be overly pessimistic, we actually want to defer the calculation to at least 8s into the slot, when we see attestation aggregates: Otherwise, the term $- (T-t+1)W$ will have grown in the negative direction, but $v(b)^t + v(b)^{t-1}$ will not have increased. Votes from a slot are observed `8 sec` into the slot - attesters gossip individual votes at the `4 sec` mark in aggregation subnets, and aggregators gossip the aggregate votes to all nodes at the `8 sec` mark. The rule should thus be applied between 8 and 12 seconds into the slot only, and the result should be frozen for the first 8 seconds of every slot. #### Early aggregation subnets Attestations are sent after 4s, but only available on subnets until they are aggregated at 8s. Only at this time are they visible to general full nodes that don't follow all attestation subnets. We therefore suggest adding a new subnet `beacon_early_aggregate_and_proof`, which has the exact same rules as `beacon_aggregate_and_proof`, but allows propagation of one "early" aggregation per aggregator. This allows them to propagate an early aggregation so that nodes can determine the safe head. This will allow evaluating the safe head rule earlier and get good confirmation earlier in the slot. ## Safe Block Rule for Checkpoint Blocks For checkpoint blocks *before the current epoch*, that is more than 32 slots before the current slot, in addition to the regular safe head checks, an extra check is required because of the FFG component of our fork choice. The additional check is that each such checkpoint block has in the chain of $b$ has $\geq \frac{1}{3} + \beta$ fraction of FFG votes ***from the epoch of the checkpoint block*** in its support. This disallows the possibility of a competing checkpoint block being justified. ### Timing considerations This presents an additional timing consideration: the checkpoint block in the current epoch will fail this check for the first $\frac{1}{3}$rd of the current epoch. We can discount the check for the checkpoint block of the current epoch. ## Safety proof sketch Proof idea: Let block $b$ be a safe block at time $t$, where $t=4\ldots12 \pmod{12s}$. Let the time of the next slot be $t'$. At time $t'+4s$, the next committee will be voting. The chain that contains block $b$ at this time has weight at least $A-B$, and any other chain can have weight at most $P-C+W_p$. Since all votes in $A$ where known to the local node at time $T$, they have been seen by all honest nodes at time $t'+\Delta$ and thus all honest nodes will vote for a chain containing $b$. Let us assume that the adversary equivocated a $E\leq B$ of the stake. We denote with a prime the safe block variables (with respect to $b$) at time $T+8s$: $A' = A - E + (\frac{1}{2}+\epsilon) W$ for some $\epsilon>0$ $C' = C + (\frac{1}{2}+\tilde \epsilon) W$ for some $\tilde \epsilon > \epsilon$ $P' = P + W$ $B'=B-E$ (The adversary has already used $E$ equivocations, so $B$ has to be reduced) Thus $A'-B'=A + (\frac{1}{2}+\epsilon) W - B >P'-C'+W_p = P+W-C-(\frac{1}{2}+\tilde \epsilon) W+W_p$ Since safe block property implies being on the fork choice, this means: 1. $b$ remains on the fork choice 2. $b$ remains a safe block, so the argument can be applied recursively to show that $b$ will remain a safe block and on the fork choice indefinitely **TODO**: Consider the influence of LMD In the LMD case, the a number of the votes (at most $W$) will be reassigned in the new committee. Let $R$ denote the number of reassigned votes from all slots, and $S \leq R$ the number of these votes that come from $A$, and $Q \leq R$ ($Q \geq S$) the number that comes from $C$. Now $P'=P+W-R$; also $A' = A - E - S + (\frac{1}{2}+\epsilon) W$ for some $\epsilon>0$ $C' = C - Q + (\frac{1}{2}+\tilde \epsilon) W$ for some $\tilde \epsilon > \epsilon$ Thus $A'-B'=A - S+(\frac{1}{2}+\epsilon) W - B \stackrel{?}{>}P'-C'+W_p = P+W-R-C+Q-(\frac{1}{2}+\tilde \epsilon) W+W_p$ Knowing $A-B > P-C+W_p$, it remains to check $- S+(\frac{1}{2}+\epsilon) W \stackrel{?}{>}W-R+Q-(\frac{1}{2}+\tilde \epsilon) W$ or $(\epsilon+ \tilde \epsilon) W \stackrel{?}{>}S+Q-R$