# evm384 (EVM + 384-bit arithmetic) **This is a small experiment from the [Ewasm](https://github.com/ewasm) team** [toc] ### Abstract Introduce three operations: - addmod384 - submod384 - mulmodmont384 These operations can be implemented at least in three different ways: 1. As opcodes operating on memory 2. As opcodes operating on stack items (2 stack items needed to represent a 384-bit number) 3. As separate precompiles `mulmodmont384` due to its complexity seems unfeasible to be implemented on EVM with good performance, but some potential shows for `addmod384` and `submod384` as discussed in the last section. ### Motivation Introduce low-level 384-bit arithmetic primitives, which can be used to implement support for new elliptic curves, such as the popular BLS12-381 curve used by Eth2.0, among others. 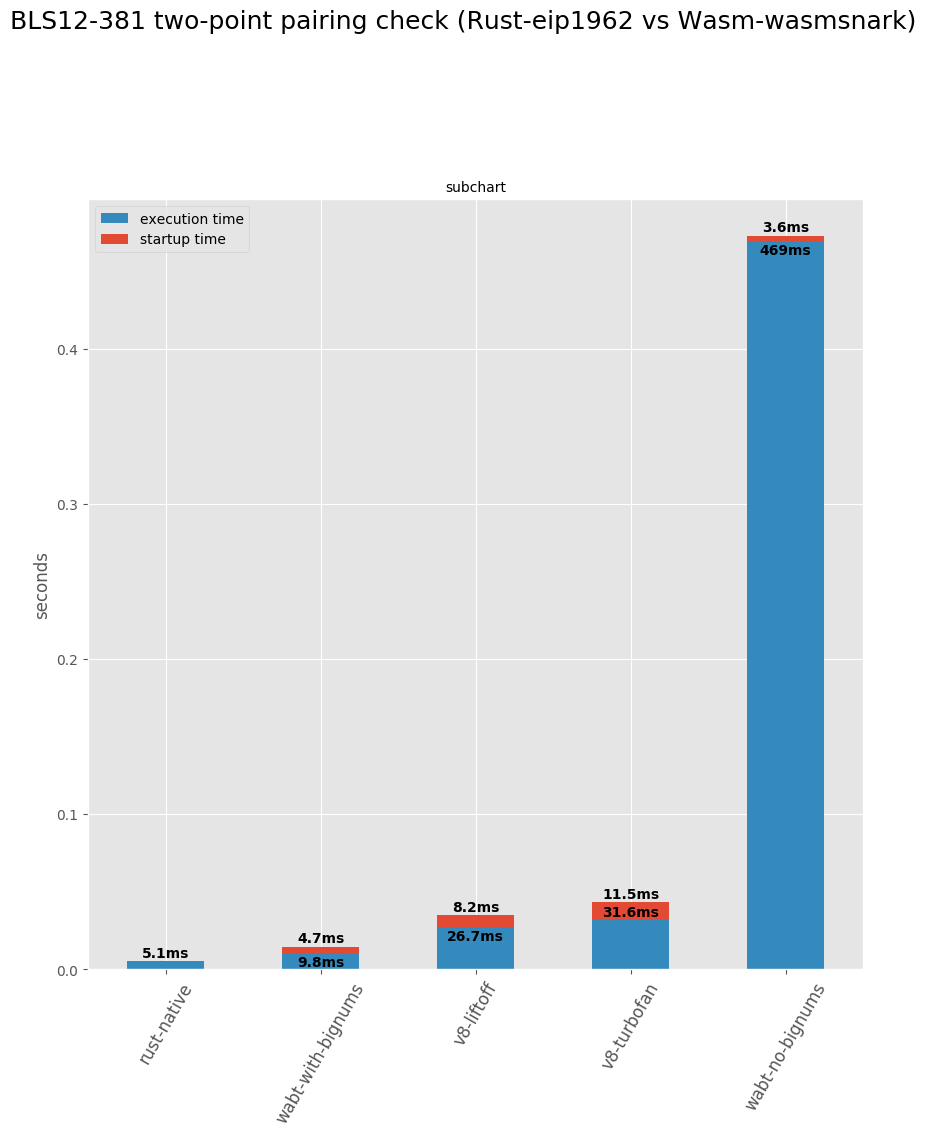### Rationale 1. (Link to Ewasm benchmarking report) Benchmarking has shown that with well designed "host functions" (aka the ones discussed in this document) it is possible to achieve near native speeds for BLS12-381 operations in WebAssembly versus native code. A two-point pairing operation can be processed in WebAssembly within 14.5ms, while it takes 5.1ms with native code. Without host functions the same takes about 469ms. ([see Wasm benchmark charts below](#Appendix-Wasm-benchmarks)) 2. TBD Rationale for `mulmodmont384` vs. `mulmod384`. ### Specification: Operating on memory (option 1) - addmod384(x, y, mod) - opcode: 0xc0 - submod384(x, y, mod) - opcode: 0xc1 - mulmodmont384(x, y, mod, r_inv) - opcode: 0xc2 where the leftmost argument is the top element on the stack (aka [Yul](https://solidity.readthedocs.io/en/v0.6.7/yul.html) notation). The `x`, `y` and `mod` arguments are offsets in memory. Each instruction will read 48-bytes from `x`, 48-bytes from `y`, and 48-bytes from `mod`. The `r_inv` argument is value restricted to 64-bits. Any `r_inv` larger than 2^64-1 will result in an exceptional halt. The result will be placed at the offset pointed by `x`. **Note:** We may change the interface to introduce an `out` offset. If we do, it may or may not allow overlapping memory with `x`, `y`, or `mod`. > We should have an implementer's note about overlapping inputs, clobbering inputs with output, and bugs. [name=Paul D.] **Question:** What to do with the `mod = 0` case? Return 0 to be aligned with the addmod/mulmod EVM opcodes? Exceptional halt? **Question:** Currently `mulmodmont384` should only work with odd `m` values. **TODO**: Figure out if different implementations of montgomery multiplication would disagree on even `m` values. If so, should we halt on those or specify the algorithm as part of the spec? > We should consider having the algorithm in the spec. This avoids possibly expensive restrictions on `mod` and `r_inv`. Then garbage-in would give canonical garbage-out. [name=Paul D.] #### Pricing Given these instructions operate on memory, the same gas semantics apply here as others operating on memory, such as `mload` and `mstore`. Additionally we set the base gas costs as (TBD): - addmod384 -- same as addmod (8 gas) - submod384 -- same as submod (8 gas) - mulmodmont -- calculate this based off the modexp precompile? (lets choose 24 gas) > I think that for arbitrary inputs, addmod384 and submod384 may be as expensive as div (to compute a remainder). Luckily, many crypto use-cases don't take arbitrary inputs, for example, inputs are less than the modulus. For these use-cases, we can build addmod and submod from inexpensive add, sub, and less_than_or_equal. [name=Paul D.] #### Implementation Without the `out` parameter: - evmone: https://github.com/axic/evmone/tree/evm384 - solc: https://github.com/ethereum/solidity/tree/evm384 With the `out` parameter (first argument): - evmone: https://github.com/axic/evmone/tree/evm384-v2 - solc: https://github.com/ethereum/solidity/tree/evm384-v2 **Note:** the evmone implementation uses little endian notation in the memory for the new opcodes. **Note:** Use `solc --strict-assembly <filename.yul>` to compile. ### Specification: Operating on stack (option 2) - addmod384(x_hi, x_lo, y_hi, y_lo, mod_hi, mod_lo) -> o_hi, o_lo - opcode: 0xc0 - submod384(x_hi, x_lo, y_hi, y_lo, mod_hi, mod_lo) -> o_hi, o_lo - opcode: 0xc1 - mulmodmont384(x_hi, x_lo, y_hi, y_lo, mod_inv_hi, mod_inv_lo) -> o_hi, o_lo - opcode: 0xc2 The `_lo` items contain the least-significant 256 bits and the `_hi` items contain the most-significant 128 bits of the 384-bit value. In the case of `mod_inv_hi` the least-significant 64 bits of the top 96 bits are used for the `r_inv` value (e.g. `mod_inv_hi = (mod >> 256) | (r_inv << 128)` where `r_inv < 2^64`) #### Implementation - evmone: not yet - solc: https://github.com/ethereum/solidity/tree/evm384-v3 ### Specification: Precompile (option 3) TBA: Alternate option is to provide these opcodes as precompiles. It seems feasible to support these as precompiles if we compare them to the opcodes-with-memory case. The two downsides: 1. Depends on a gas reducing change, such as EIP-2046. 2. The`r_inv` argument has to be encoded in memory, and all arguments have to be a contiguous memory area for efficiently passing data back-and-forth between the precompile invocations (e.g. without doing memory copying in EVM). ### BLS12-381 benchmarking We have created some synthetic benchmarks based on the BLS12-381 pairing operation in [wasmsnark](https://github.com/iden3/wasmsnark). This benchmark tries to approximate the complexity of the real pairing operation, but is implementable within a reasonable timeframe on EVM. To this end we have it implemented in using wasmsnark and in EVM (using Yul): https://github.com/ewasm/evm384_f6m_mul ### Appendix: Wasm benchmarks These numbers are noisy (only two repetitions). Should look better after a full run.