--- tags: defi --- # Uniswap and Constant Product Market Makers (CPMM) There are two assets, X and Y. Denote by $x$ the volume of X and by $y$ the volume of Y in the reserves. The relationship $$ xy = k $$ means that the price is determined based on the constant factor $k$. Uniswap is called _constant product_, but there are more general instantiations (_constant function_). ## Basic operations ### Trades When a user comes to exchange some quantity $\Delta x$ of X against $\Delta y$ of Y, the user receives $\Delta y$ such that $$ (x + \Delta x) (y - \Delta y) = k = xy $$ i.e., $$ \Delta y = \frac{y \cdot \Delta x}{x + \Delta x}$$ This is true when the pool does not take a fee on the transaction. In general, the user also pays a fee at rate $(1-\gamma)$ to the pool, $\gamma \in [0, 1]$, i.e., the user sends $\Delta x$, receives $\Delta y$ such that $$ (x + \gamma \Delta x) (y - \Delta y) = k = xy $$ so the user receives $$ \Delta y = \frac{y \cdot \gamma \Delta x}{x + \gamma \Delta x} $$ The constant factor of the pool after a trade is updated to $$ k' = (x + \Delta x) (y - \Delta y) > (x + \gamma \Delta x) (y - \Delta y) = k $$ ### Liquidity providing A liquidity provider adds volume to the market, by adding $\Delta x$ amount of X and $\Delta y$ amount of Y. The liquidity factor is $\alpha = \frac{\Delta x}{x}$. Whenever a LP adds $\Delta x$ X tokens, they must also add $\Delta y$ Y tokens such that $$ y + \Delta y = (1+\alpha) y $$ i.e. $$ \Delta y = \alpha y = \frac{\Delta x}{x} y $$ Calling $p_{X \rightarrow Y} = \frac{y}{x}$, we find $\Delta y = \Delta x \cdot p_{X \rightarrow Y}$, i.e., the liquidity provider deposits equivalent amounts of X and Y _at the price of the pool_. The LP receives LP tokens accounting for their contribution to the pool. If $t$ tokens were previously minted, they receive $\Delta t = \alpha t$ tokens in return, minted to them. Note that the constant factor of the pool changes after liquidity providing. $$ k' = (x + \Delta x) (y + \Delta y) > xy = k $$ ### Removing liquidity When the LP removes $\Delta x$ from the pool, they receive $\Delta y$ and burn an equivalent amount of liquidity tokens they own $\Delta t$. This time let $\alpha = \frac{\Delta t}{t}$. The LP is entitled to retrieve $\alpha x$ and $\alpha y$ from the pool. The pool returns to the same state if a LP mints $\Delta t$ then burns $\Delta t$ tokens, and the LP balances are the same before and after the process. See [Runtime Verification's audit](https://github.com/runtimeverification/verified-smart-contracts/blob/uniswap/uniswap/x-y-k.pdf). ### First liquidity provider From [Uniswap v2 whitepaper](https://uniswap.org/whitepaper.pdf).  ## Impermanent loss and arbitrage Impermanent loss describes a loss realised whenever the LP removes liquidity at a price different from the price when the liquidity was added. Suppose the reserves are $x$ and $y$, $t$ LP tokens were minted, of which the LP owns $\Delta t$. The LP had deposited the liquidity when price was $p_{X \rightarrow Y}$. ### Arbitrage example Suppose the new price is $p_{X \rightarrow Y}' < p_{X \rightarrow Y}$, where $p_{X \rightarrow Y}'$ is quoted by another exchange. A trader can arbitrage between $p_{X \rightarrow Y}$, the price in the pool, and $p_{X \rightarrow Y}'$, the price in the exchange. In the pool, one unit of X gets you $p_{X \rightarrow Y}$ units of Y. In the exchange, one unit of X gets you $p_{X \rightarrow Y}'$ units of Y. 1. The trader goes to the pool to buy cheap Y with X, with $\Delta x$ units of X that they borrowed from somewhere. 2. The trader receives $\Delta y = \frac{y \cdot \gamma \Delta x}{x + \gamma \Delta x}$. 3. The trader goes to the exchange to get $\Delta x'$ units of X in exchange of $\Delta y$ units of Y, at price $p'_{Y \rightarrow X} = \frac{1}{p_{X \rightarrow Y}'}$, i.e. $\Delta x' = \frac{\Delta y}{p_{X \rightarrow Y}'}$. An example: suppose X is ETH and Y is DAI. The pool has 100 ETH and 10,000 DAI, hence, $p_{ETH \rightarrow DAI} = 100$, so 1 ETH gets you 100 DAI, while on the exchange, $p_{ETH \rightarrow DAI}' = 50$, so 1 ETH gets you 50 DAI. 1. The trader borrows $\Delta x$ = 1 unit of ETH. 2. The trader buys $\Delta y$ unit of DAI, receiving $\Delta y = \frac{10000 \cdot 0.997 \cdot 1}{100 + 0.997 \cdot 1} = \frac{9970}{100.997} = 98.72$ DAI. 3. The trader goes to the exchange, and buys $\Delta x'$ units of ETH with their $\Delta y$ units of DAI. Since the price is $p_{DAI \rightarrow ETH}' = \frac{1}{p_{ETH \rightarrow DAI}'} = \frac{1}{50} = 0.02$, the trader receives 1.9744 ETH. 4. The trader reimburses 1 ETH to the loaner and keeps 0.9744 ETH. Note that this is profitable to do so as long as $\Delta x' > \Delta x$, i.e., $$ J(\Delta y) = \frac{1}{p_{X \rightarrow Y}'} \Delta y - \frac{1}{\gamma} \Big( \frac{k}{y - \Delta y} - x \Big) > 0$$ We can maximise $J$ to find the most profitable quantity $\Delta y$ to buy from Uniswap. This yields $$\Delta y = y - \sqrt{\frac{k p_{X \rightarrow Y}'}{\gamma}}$$ Then $$\Delta x = \sqrt{\frac{k}{\gamma p_{X \rightarrow Y}'}} - \frac{x}{\gamma}$$ See [optimal arbitrage](https://web.stanford.edu/~guillean/papers/uniswap_analysis.pdf). ### Computing impermanent loss Assume I am a LP to the pool before the trader comes and does that trade. I added 1 ETH and 100 DAI and so I own 1 share out of a 100 minted by the pool. After the trade, the pool balances are | ETH | DAI | |-|-| | 101 | 9901.28 | Suppose I burn my share to retrieve my liquidity. I receive: | | ETH | DAI | Total | |-|-|-|-| | Nominal | 1.01 | 99.0128 | x | | USD | 1.01 * 50 = 50.5 | 99.0128 | 149.5128 | This is worse than if the LP had simply kept their 1 ETH and 100 DAI! | | ETH | DAI | Total | |-|-|-|-| | Nominal | 1 | 100 | x | | USD | 1 * 50 = 50 | 100 | 150 | There is also a loss in the other direction, if $p_{X \rightarrow Y}' > p_{X \rightarrow Y}$. Given the pool price $p_{X \rightarrow Y} = \frac{y}{x}$, assume the price shifts to $p_{X \rightarrow Y}' = \frac{x'}{y'}$ with $xy = x'y' = k$ (in practice, it wouldn't be exactly true because of fees). So we have in general $$ x = \sqrt{\frac{k}{p_{X \rightarrow Y}}}, \quad y = \sqrt{k \cdot p_{X \rightarrow Y}} $$ We denominate everything in units of Y (if Y is DAI, it's equivalent to thinking in USD terms). _At $p_{X \rightarrow Y}$_ | Pool ETH (nominal) | Pool DAI (nominal) | Value (in Y) | |-|-|-| | $x$ | $y$ | $xp_{X \rightarrow Y} + y = 2 \sqrt{k \cdot p_{X \rightarrow Y}}$ | _At $p_{X \rightarrow Y}$'_ | Pool ETH (nominal) | Pool DAI (nominal) | Value (in Y) | |-|-|-| | $x'$ | $y'$ | $x' p_{X \rightarrow Y}' + y' = 2 \sqrt{k \cdot p_{X \rightarrow Y}'}$ | _The liquidity provider owns a share $\ell$ of the pool_ Value of holding: $\ell x p_{X \rightarrow Y}' + \ell y = \ell \sqrt{\frac{k}{p_{X \rightarrow Y}}} p_{X \rightarrow Y}' + \ell \sqrt{k \cdot p_{X \rightarrow Y}}$ Value of LP: $2\ell \sqrt{k \cdot p_{X \rightarrow Y}'}$ **Relative loss:** $$ \frac{\text{Value of LP}}{\text{Value of HODL}} = \frac{2\sqrt{k \cdot p_{X \rightarrow Y}'}}{x p_{X \rightarrow Y}' + y} = \frac{2\sqrt{r}}{r + 1} $$ with $r = \frac{p_{X \rightarrow Y}'}{p_{X \rightarrow Y}}$ the price ratio. When $r=1$ there is no loss.  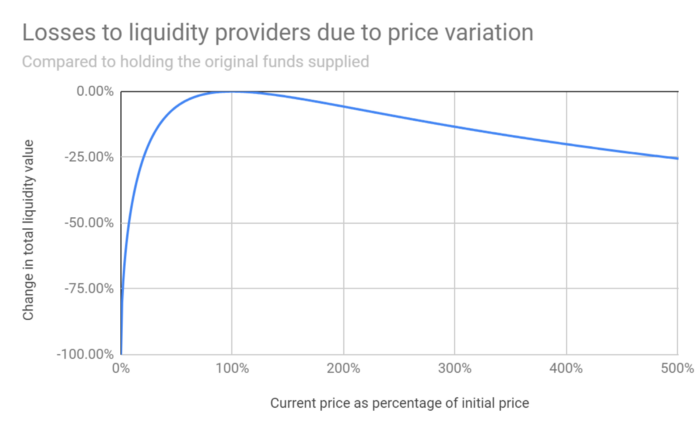See [pintail's piece](https://pintail.medium.com/uniswap-a-good-deal-for-liquidity-providers-104c0b6816f2) and [Finematics](https://finematics.com/impermanent-loss-explained/). See also [this tool](https://twitter.com/ChainsightA/status/1373394831221915653) to check for impermanent loss. ### [Sandwitch](https://www.youtube.com/watch?v=6VWKPZYaGo4)ing > Sandwitcher places one transaction before and one transaction after the target transaction. Starting pool state $(x, y)$. 1. Sandwitcher sells $\Delta x_b$ against $\Delta y_b$, so that the price of Y relative to X increases. - $k_1 \leftarrow (x + \Delta x_b) (y - \Delta y_b)$ - Receives $\Delta y_b = \frac{y \cdot \gamma \Delta x_b}{x + \gamma \Delta x_b}$ - Pool state $(x_1, y_1) = (x + \Delta x_b, y - \Delta y_b)$ 2. Target transaction: trade $\Delta x$ of X against $\Delta y$ of Y. - $k_2 \leftarrow (x_1 + \Delta x) (y_1 - \Delta y)$ - Receives $\Delta y = \frac{y_1 \cdot \gamma \Delta x}{x_1 + \gamma \Delta x}$ - Pool state $(x_2, y_2) = (x_1 + \Delta x, y_1 - \Delta y)$ 3. After target trade, they sell $\Delta y_f$ for $\Delta x_f$. - $k_3 \leftarrow (x - \Delta x_f) (y + \Delta y_f)$ - Receives $\Delta x_f = \frac{x_2 \cdot \gamma \Delta y_f}{y_2 + \gamma \Delta y_f}$ - Pool state $(x_3, y_3) = (x_2 - \Delta x_f, y_2 + \Delta y_f)$ Assume $\Delta y_b = \Delta y_f$. For the sandwitcher, optimisation problem is $$\max_{\Delta x_b} \Delta x_f - \Delta x_b$$ with $$ \begin{aligned} \Delta x_f & = \frac{x_2 \cdot \gamma \Delta y_f}{y_2 + \gamma \Delta y_f} \\ & = \frac{(x_1 + \Delta x) \cdot \gamma \Delta y_b}{(y_1 - \Delta y) + \gamma \Delta y_b} \\ & = \frac{(x_1 + \Delta x) \cdot \gamma \Delta y_b}{(y_1 - \frac{y_1 \cdot \gamma \Delta x}{x_1 + \gamma \Delta x}) + \gamma \Delta y_b} \\ & = \frac{(x + \Delta x_b + \Delta x) \cdot \gamma \frac{y \cdot \gamma \Delta x_b}{x + \gamma \Delta x_b}}{y_1(1 - \frac{\gamma \Delta x}{x_1 + \gamma \Delta x}) + \gamma \frac{y \cdot \gamma \Delta x_b}{x + \gamma \Delta x_b}} \\ & = \frac{(x + \Delta x_b + \Delta x) \cdot \gamma \frac{y \cdot \gamma \Delta x_b}{x + \gamma \Delta x_b}}{(y - \frac{y \cdot \gamma \Delta x_b}{x + \gamma \Delta x_b})(1 - \frac{\gamma \Delta x}{x + \Delta x_b + \gamma \Delta x}) + \gamma \frac{y \cdot \gamma \Delta x_b}{x + \gamma \Delta x_b}} \end{aligned} $$ Solve for $\Delta y_b$ $$\max_{\Delta y_b} \frac{(x + \Delta x_b + \Delta x) \cdot \gamma \Delta y_b}{(y - \Delta y_b)(1 - \frac{\gamma \Delta x}{x_1 + \gamma \Delta x}) + \gamma \Delta y_b}$$