# Proposer Boost considerations *Joint document by Francesco and Caspar.* We need to pick a proposer LMD score boost value, $W_{PB}$. Currently $W_{PB}$ is defined in the specs as `PROPOSER_SCORE_BOOST: 70`. General opinion is that this value is too high. On the one hand, you want the proposer boost to not be too high: The reason is that a high proposer boost enables an adversary to abuse it and do ex post reorgs or sandwich ex ante reorgs. Consider the following sandwich scenario: A 10%-adversary proposing block `n` and `n+2` can reorg block `n+1` despite the proposer boost, or in fact because of the proposer boost: 10% (adv. slot `n` votes) + 10% (adv. slot `n+2` votes) + 70% ($W_{PB}$) = 90%, which is equal to honest weight voting for block `n+1` (assuming all honest validators vote correctly etc.) On the other hand, you want proposer boost to be high enough to prevent ["simple" ex ante reorgs and balancing attacks](https://arxiv.org/abs/2110.10086). So what is the right middle ground? Let's consider the trade off space. ## ex ante reorg A 1-ex-ante reorg refers to the vanilla ex ante reorg that forks out a single honest block. We need $W_{PB}> \beta$ to protect against 1-ex-ante reorgs. Simple enough. If you want to account for a 1/3-attacker we need a proposer boost of 1/3. If we assume favorable attacking conditions with the adversary controlling $l$ blocks in a row we get: $W_{PB}>l\beta$ ## ex ante sandwich reorg To protect against a vanilla sandwich reorg attack as described in the intro, we need $W_{PB}+2\beta < 1-\beta$, put differently we need $W_{PB}<1-3\beta$. If we assume favorable attacking conditions with the adversary controlling $l-1$ blocks in a row and one afterwards, we get: $1-\beta>W_{PB}+l\beta$. The security condition being this inequality is actually only true for $l>1$. For $l=1$ there's no ex-ante component, and the sandwich is really just an ex-post reorg, which can be done by a minority adversary by abusing boost. To be safe against this we then need $W_{PB} < 1-\beta$: the additional $\beta$ from the formula above does not apply because it would come from the honest slot and the adversary does not yet have a block to vote for (again, the ex-ante component is missing) ## balancing attack To be protected against balancing attacks in expectation we need the following to hold: $[(1-\beta) min(1-\beta,W_{PB})]-[\beta min(1-\beta,W_{PB})+\beta]>0$. Intuition for this inequality is this: First term represents the number of attestations that the honest validators accumulate, whereas the second term represents the accumulation of adversarial voting power. We need the honest votes to dominate the adversarial votes. The $min(1-\beta,W_{PB})$-term chooses the smaller value between the honest fraction and the boost value, because that is what the adversary will choose to overpower to keep the balancing going. With this in mind and assuming e.g. $(1-\beta) = 0.8$ and $W_{PB} = 0.7$ we get: With probability $(1-\beta)$ the honest validators control the slot and gain $W_{PB}$ votes. With probability $\beta$ the adversary controls a slot in which case they get a boost worth $W_{PB}$ votes as well as the $\beta$ adversarial votes (validators they control in that slot). Note that the honest validators don't gain $(1-\beta)$ votes in an honest slot, because they get balanced by the adversary! ## Putting it all together We are still considering the attacker only controls the minimal amount of slots such that the attacks are feasible. In a moment we'll also consider more favorable attacking conditions: The adversary may control several blocks in a row such that they can accumulate votes to be used in the attack. [The plot can be played around with here](https://www.desmos.com/calculator/irqjqnvnwq). The following plots the above inequalities. We want to be in the intersection of all colored sets. The plot suggests we can protect against ex-ante+balancing attacks for any $W_{PB}<\beta$ (and against sandwich attacks by the $l=1$-assumption). 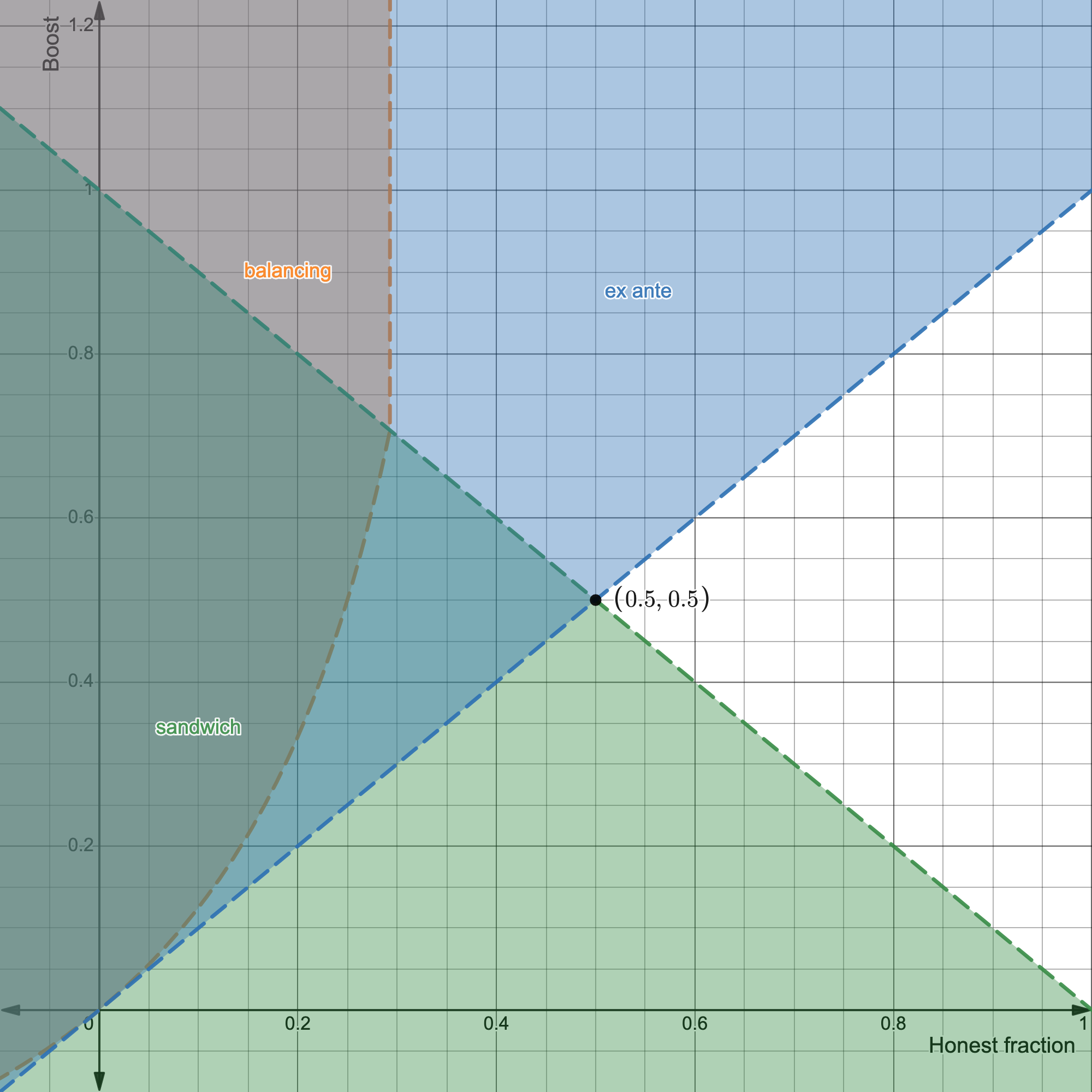Adversary controlling one block, $l=1$:  The plot suggests $W_{PB}=0.5$ to protect against ex-ante and sandwich reorgs with $l=1$, ignoring long-term balancing attacks. Given the incentives at play, it may be reasonable to prioritize reorg protection. 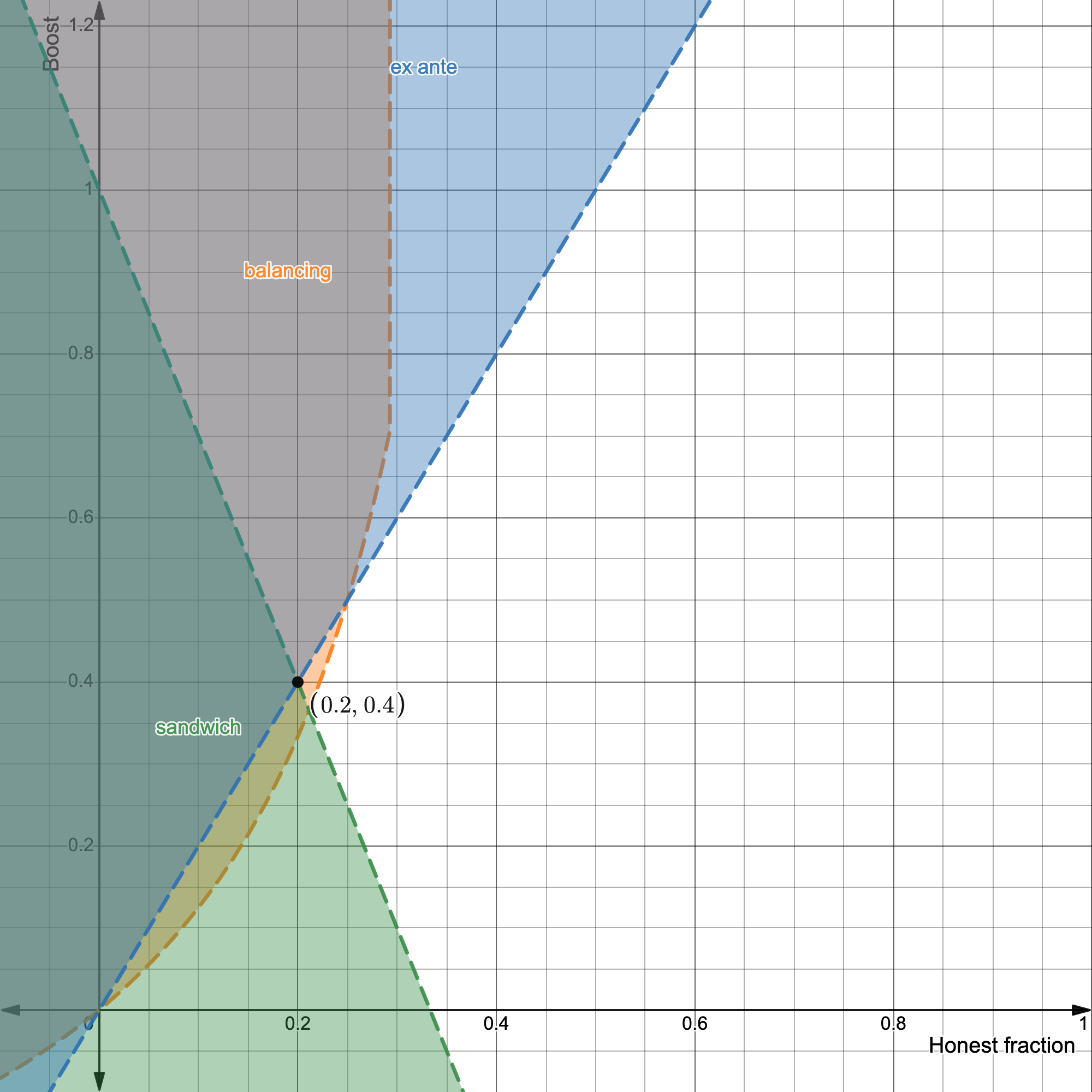Adversary controlling two blocks in a row, $l=2$:  This suggests that for $l=2$ we have an optimal ex-ante+sandwich+balancing protection against $<20\%$ attackers by choosing $W_{PB}=0.4$. 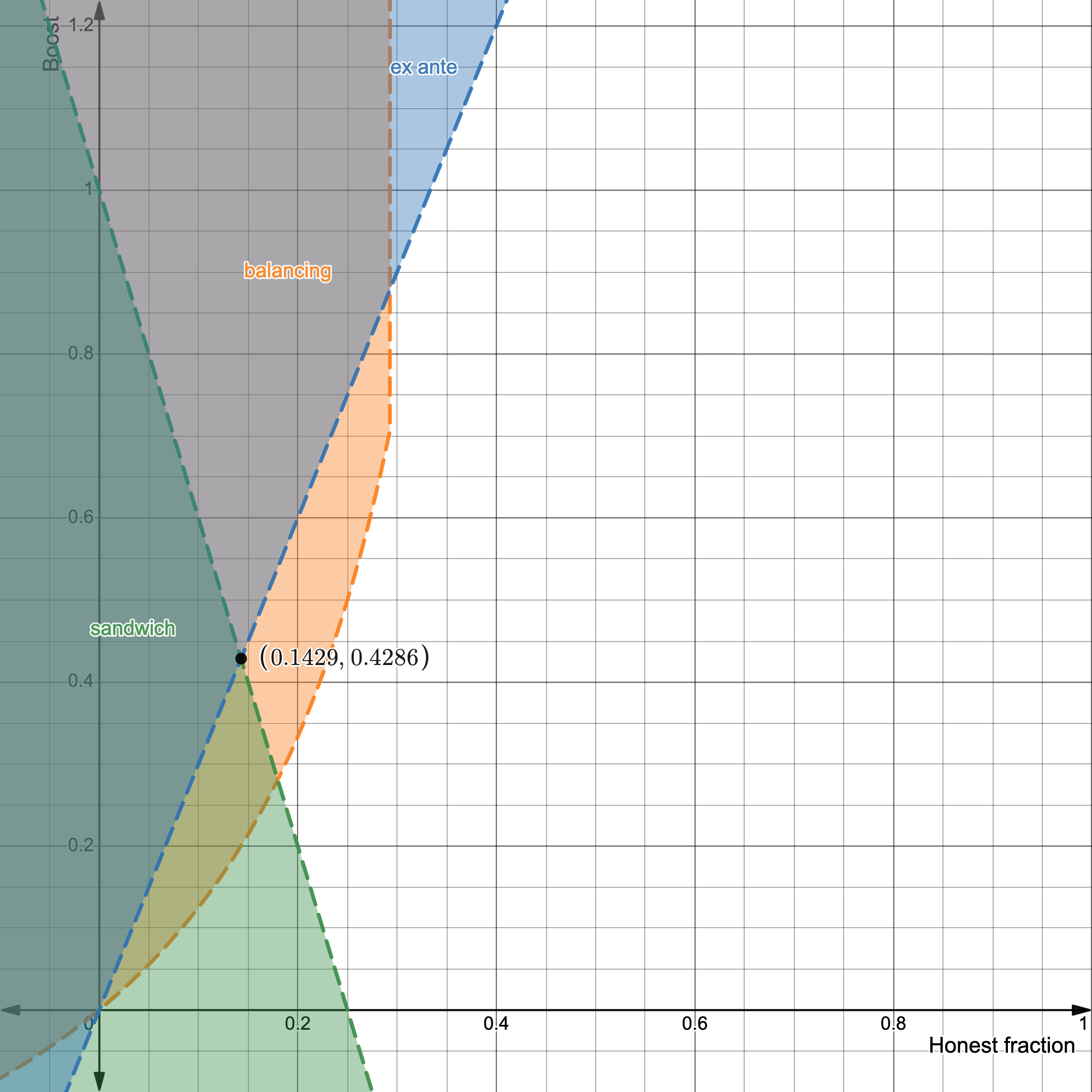Adversary controlling three blocks in a row, $l=3$:  This suggests that for $l=3$ we get ex-ante+sandwich+balancing protection against $<14.3\%$ attackers with a boost of $W_{PB}=0.43$. Similarly, for $l=4$ we get ex-ante+sandwich+balancing protection against $<11.1\%$ attackers with a boost of $W_{PB}=0.44$. ### Considering reorg frequencies to choose $W_{PB}$ Essentially there is a tradeoff between protecting against smaller adversaries with favorable attacking conditions (i.e. controlling multiple blocks in a row) vs. protecting against larger adversaries at all. If we want to be safe against smaller adversaries that control several blocks in a row we need a higher boost value $W_{PB}$. But a higher $W_{PB}$ allows larger adversaries to do sandwich reorgs more easily. So it's a question of what we want to be better protected against: smaller adversaries with favorable attacking conditions or be safe at all with larger adversaries. Here are some useful things to keep in mind as we explore the tradeoff-space and try to come up with a reasonable value: - We should not concern ourselves with reorgs which we cannot prevent: to every $l$-reorg class corresponds a maximum $\beta$ which we can defend against, i.e. for which there exists a boost value that prevents such reorgs (the extreme points in the plots are such values), and there is nothing we can do about stronger adversaries *for this reorg class*. - $l=1$ reorgs are the most dangerous in theory, because they are most frequent, but in practice they are not possible for any reasonable adversary, as long as we choose boost high enough, i.e. $> \beta$ and $< 0.5$. We can then ignore 1-reorgs as long as the boost value we choose is higher than the maximum adversary we are worried about. Given that optimal boost values to protect against $l=2$ and $l=3$ reorgs are $W_{PB} = 0.4$ and $W_{PB} = 0.43$, $l=1$ reorgs are practically not concerning. - $l=2$ reorgs are then practically the most concerning ones, because they are still fairly frequent even for reasonably sized adversaries, e.g. a $10\%$-adversary has the right condition to do one 1% of the time, i.e. when they control two blocks either before or "around" the honest block (this does not mean that the reorg can actually be carried out, as that depends on what boost value we choose). More importantly, the maximum adversary which we can "defend against at $l=2$" is $\beta = 0.2$, and a $20\%$-adversary can do a 2-reorg once every 25 blocks, more than once an epoch! - $l=3$ reorgs are still "relevant" in terms of frequency: the maximum adversary which we can defend against at $l=3$ is $\beta = 0.143$, which can do a 3-reorg every 340 blocks, i.e. once every 5 epochs, or twice an hour. - $l=4$ reorgs are essentially irrelevant in terms of frequency, *for all adversaries which we can in principle defend against*, i.e. $\beta < 0.11$. Such an adversary can do a reorg roughly every 7000 slots, i.e. roughly once a day (not irrelevant, but irrelevant relative to other reorg classes). Clearly, this also then applies (and even more so) to $l > 4$. This would suggest that we should choose a boost value which works well against $l=2$ and $l=3$ reorgs. Let's start with the two values which are optimal for $l=2$ and $l=3$, respectively, i.e. $0.4$ and $0.43$. How do they work for "the other" reorg classes? To check this, we need to compute the maximum $\beta$ which a certain boost value protects against "at a certain $l$". It's easy to show that this is how to do it: ```python def max_beta(boost, l): if l == 1: return min(1/2, boost) else: return min(boost/l, (1-boost)/(l+1)) ``` $W_{PB} = 0.4$ protects against 2-reorgs by $\beta = 0.2$ adversaries (as we already knew from the plot), and we can now compute that $W_{PB} = 0.43$ protects against $\beta = 0.19$ adversaries at $l=2$, quite close. Similarly, $W_{PB} = 0.4$ at $l=3$ protects against $\beta = 0.133$ adversaries, whereas the optimal value $W_{PB} = 0.43$ protects against $\beta = 0.143$ adversaries. We can already see that these values work almost identically at both $l=2$ and $l=3$, with only a minor tradeoff, so they are intuitively good candidates to be chosen. To confirm this intuition, we can extend this reasoning to evaluate a whole range of boost values, simply by computing what percentage of all blocks can be reorged with a given boost value, for a variety of adversaries. For a given $(\beta, W_{PB})$-pair, we compute `cumulative_reorg_percentage(beta, boost)`, the percentage of blocks which a $\beta$ adversary can reorg with this $W_{PB}$, through $l$-reorgs for $l \in \{1,2,3\}$. In practice, $l=1$ and $l=4$ are irrelevant, as already discussed above. The table below shows the results of this computation, for boost values $\in [0.37, 0.46]$ and $\beta \in [0.1, 0.24]$. Each column corresponds to a boost value, and shows the cumulative reorg percentage for a variety of adversaries, so comparing columns is a way to compare boost values. Note on how to understand the table and on the choice of $\beta$ values: the reason why the table does not contain higher values of $\beta$ is that we cannot protect against those $\beta$ at $l=2$, so there's "nothing interesting" happening for those values. At $\beta = 0.2$, $l=2$ reorgs become impossible do defend against, and nothing changes afterwards. The next "critical point" would be when $l=1$ reorgs come into play, but that's for values of $\beta$ which are too high for us to care. 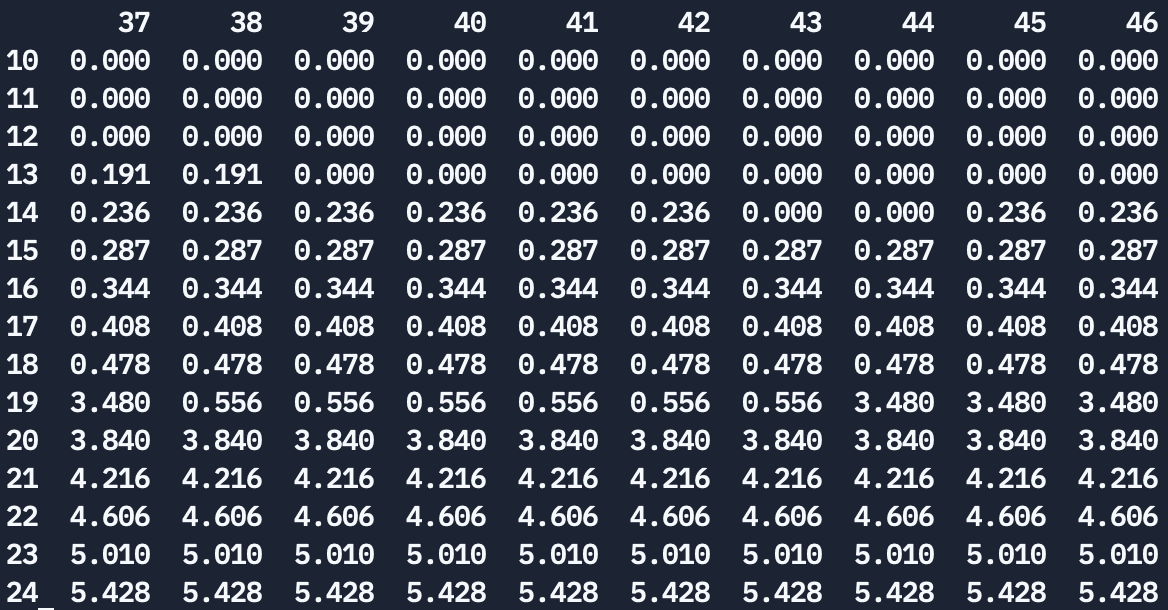Similarly, the other "critical point" in the table is for $\beta = 0.15$, when $l=3$ become impossible to defend against, so all boost values perform similarly until we get to adversaries for which $l=2$ reorgs become possible (and since we have chosen a reasonable range of boost values to analyze, this happens almost all at once, for $W_{PB} = 0.19$)  The table suggests that $W_{PB}=0.43$ is the best proposer boost value, but values are discrete and after all it's a decision whether we want to be better protected against larger adversaries or smaller adversaries with favourable attacking conditions. Any value $W_{PB} \in [0.4, 0.43]$ seems reasonable. Note that considering $l\geq4$ would add some rounding errors, but we are talking about frequencies of roughly once per day and less. Feel free to play around with the code computing the above [here](https://replit.com/@casparschwa/DisloyalExcitableMathematics#main.py). ### Conclusion $W_{PB}=0.4$ optimally protects against reorgs by $20\%$-adversaries with $l=2$, while minimally trading off for $l=3$ by protecting against $\beta \leq 0.133$ adversaries, as opposed to the optimal $l=3$ protection against $\beta\leq0.143$ adversaries as achieved by $W_{PB}=0.43$. By choosing $W_{PB}=0.4$ over higher boost values such as $W_{PB}=0.43$ we are slightly better protected against larger adversaries in $l=2$ settings, at the expense of being slightly less protected in $l=3$ settings. A reasonable tradeoff. We think any value $W_{PB} \in [0.4, 0.43]$ is reasonable, with a minor preference for $W_{PB} = 0.4$.