# Bouncing attack v2 ## Background: Ethresearch discussions: https://ethresear.ch/t/analysis-of-bouncing-attack-on-ffg/6113 https://ethresear.ch/t/prevention-of-bouncing-attack-on-ffg/6114 Current fix: ```python def should_update_justified_checkpoint(store: Store, new_justified_checkpoint: Checkpoint) -> bool: """ To address the bouncing attack, only update conflicting justified checkpoints in the fork choice if in the early slots of the epoch. Otherwise, delay incorporation of new justified checkpoint until next epoch boundary. See https://ethresear.ch/t/prevention-of-bouncing-attack-on-ffg/6114 for more detailed analysis and discussion. """ if compute_slots_since_epoch_start(get_current_slot(store)) < SAFE_SLOTS_TO_UPDATE_JUSTIFIED: return True justified_slot = compute_start_slot_at_epoch(store.justified_checkpoint.epoch) if not get_ancestor(store, new_justified_checkpoint.root, justified_slot) == store.justified_checkpoint.root: return False return True ``` ## (Not really) new version of the attack The second ethresearch post already discusses the fact that an adversary with granular control of message timing can still carry out the attack after the fix. In fact, an adversary can apply the same methodology from the balancing attack described [here](https://ethresear.ch/t/attacking-gasper-without-adversarial-network-delay/10187) and obtain the same result. In particular, if the pre-conditions for a bouncing attack are in place, an adversary with a very small fraction of the stake can still carry out the attack and prevent finality indefinitely, even with the current fix. To see how, let's first set the assumptions: - The adversary has a fraction $\beta < \frac{1}{3}$ of the stake - The deadline to incorporate new justified checkpoint during an epoch is after a fraction $p$ of the slots in the epoch. Here we take $p$ to be continuous, though in reality it can only be a multiple of $\frac{1}{32}$ - The adversary releases the messages which reveal a new justified checkpoint in such a way that a fraction $q$ of honest attesters see them after the deadline and $1 - q$ before. The initial target of FFG votes (C'' in the image from ethresearch) then accrues these honest votes throughout the epoch: $(1-\beta)p + (1 - \beta)(1-p)q$. The adversary can raise the total to up to $(1-\beta)p + (1 - \beta)(1-p)q + \beta$. For the attack to succeed, the first needs to be < 2/3 (not justified), and the latter > 2/3 (justifiable) Assume first that $(1-\beta)p <2/3$. Then we have $(1-\beta)p < 2/3 < 1-\beta = (1 - \beta)(p + (1-p))$. It follows that there exists a $q \in [0,1]$ s.t. $2/3 - (1-\beta)(p + (1-p)q) < \beta$ (justifiable) and $(1-\beta)(p + (1-p)q) < 2/3$ (not justified). The intuition is simply that $a = (1-\beta)p$ are the honest votes up to the deadline, which the adversary here does not attempt to control in any way, whereas $b = (1-\beta)(1 - p)$ are the votes after the deadline, which the adversary can exert granular control over through $q$, in particular by controlling what fraction of these go to $C''$, and making this fraction be just enough for the justifiable-but-not-justified condition. As long as $a < 2/3$, and since $a + b > 2/3$ because it equals all honest votes, the adversary can then set $q$ so that $a + bq$ is less than $2/3$ but within $\beta$ of it, and thus $C''$ is justifiable but not justified. If instead $(1-\beta)p \geq 2/3$, the adversary can instead just release the sway messages at a fraction $p' < p$ of the epoch, which is such that $(1- \beta)p'$ satisfies the justifiable-but-not-justified condition. ## Example For concreteness, let's discuss the case $\beta = 1/10$, $p = 1/4$ (this corresponds to our current fix). $(1-\beta)p = 0.9*0.25 = 0.225$, and with $q = 0.51$ we get $(1-\beta)(p + (1-p)q) = 0.225 + 0.675*0.51 = 0.57$, which is what we need for the justifiable-but-not-justified condition with $\beta = 0.1$. Things would actually work for any $q \in [0.51, 0.65]$, so the adversary has quite a bit of slack. For $\beta = 1/3$, any $q > 0.5$ would work for any $p$. In general, the smaller the adversary, the smaller the range of $q$ which works ## Proposed fixes A fix could use proposers for synchronization, as in [proposer view-merge](https://ethresear.ch/t/change-fork-choice-rule-to-mitigate-balancing-and-reorging-attacks/11127) proposal for an alternative fix to balancing attacks, by syncing views around the SAFE_SLOTS_TO_UPDATE_JUSTIFIED deadline (I'll just use the current value, i.e. 8, from now on). Basically, validators which have seen justification evidence for the new checkpoint before slot 7 will process it, and then only further do so in slot 8 if it the justified checkpoint has been updated in the proposal of slot 8. This way, a honest proposer in slot 8 would sync up views. Basically, do this: https://github.com/ethereum/consensus-specs/compare/dev...fradamt:consensus-specs:patch-1, and in addition change the behavior of the proposer of slot 8 to still update justified throughout slot 7 ## Worse proposed fix (here just in case there's something wrong with the one above, but otherwise that one is better) A separate proposer-view-merge at the checkpoint level. A strawman proposal for how this could work is as follows: - New justified checkpoints received in slots 1 up to 31 of epoch n are cached and only incorporated at the beginning of epoch n+1 - New justified checkpoints received in slot 32 of epoch n are cached and only incorporated at the beginning of epoch n+2. - If the first proposer of epoch n+1 builds on a justified checkpoint which has been cached for epoch n+2, i.e. which has been received in the previous slot, incorporate the checkpoint before running the fork-choice This way, the first proposer of an epoch has one whole slot to see checkpoints which have been revealed just around the deadline, and is able to incorporate them and get everyone on their view. If a checkpoint is instead revealed so late that the first proposer doesn't see it, it should be the case that most validators have also seen it later than slot 31 of the last epoch, and won't consider it during the current one. ## Bouncing + balancing attack (no fix here... but need weird setup and roughly 20% attacker) There is another (admittedly very contrived) attack which can be done even with the proposed fixes, by combining balancing and bouncing. To start it, one needs two chains, one with a justifiable-but-not-justified checkpoint (JNJ) (the bottom one in the picture), and one where the there's a balancing going on, and the adversary has accumulated many unused attestations. Using the latter, the adversary can perform an ex-ante reorg at the beginning of an epoch, which lets a new JNJ checkpoint be created with minimal use of their own attestations. These can thus be saved and later used on the second chain. At this point we have the same setup as the beginning, but with the roles of the two chains inverted (JNJ on first chain, saved attestations on the second one), and we can repeat the attack.  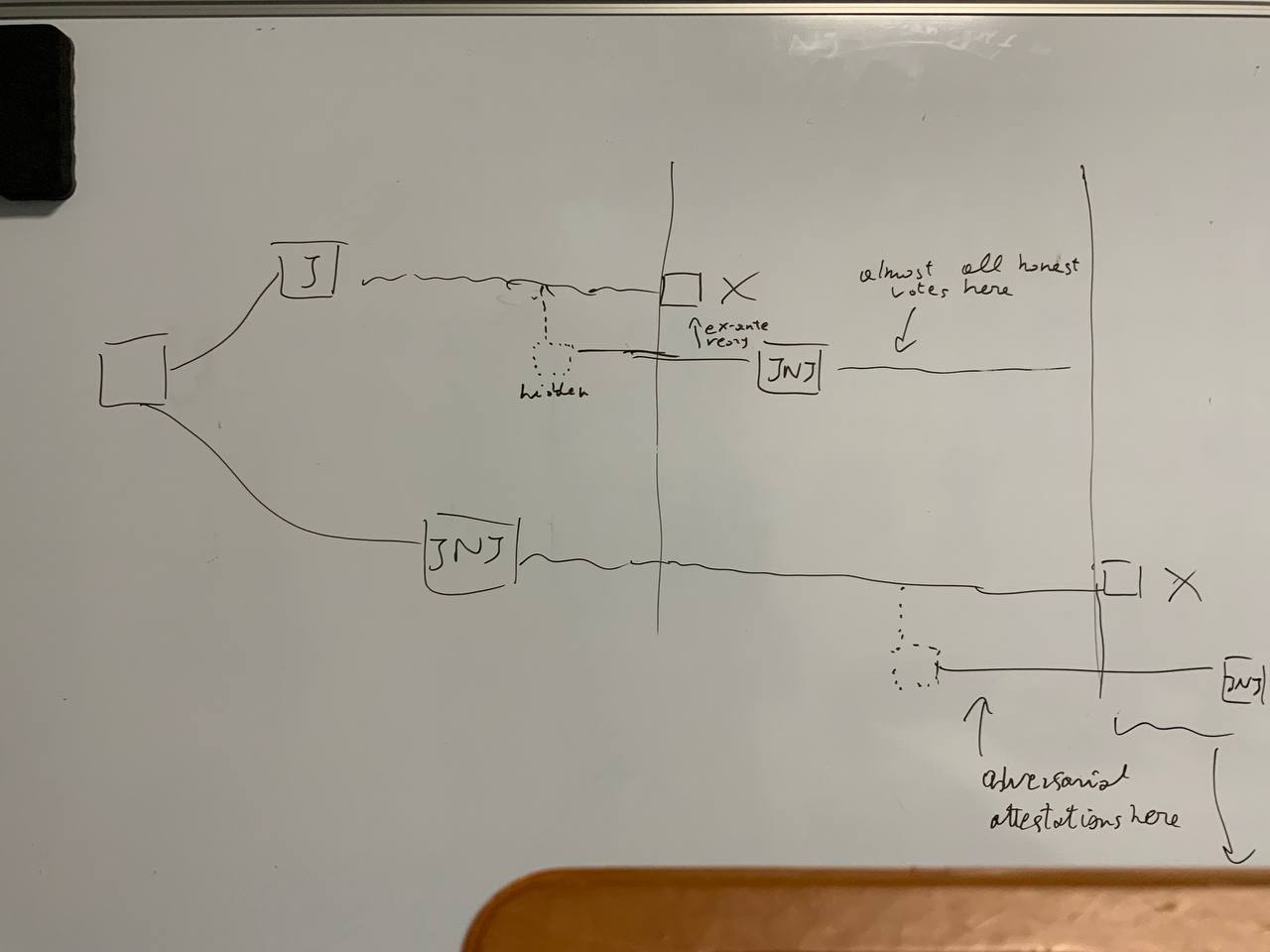Let's say the attacker has p% stake. They need to do the ex-ante reorg after k blocks, where (1-p)*(32-k)/32 < 2/3. Say 1-p = m*p. Then they need mk+1 blocks. With p = 0.2 that's 25 (best k for the attacker is 6), so still doable, but can't go much lower. Not super concerning, but it does prevent a proof of liveness for Gasper with proposer-view-merge. If this interplay of balancing and bouncing can be dealt with, I think a proof of liveness would be possible (it would be possible if the only reorgs were through LMD-GHOST votes and not also through FFG votes)