Chained isolated 3SF protocol

Casper-FFG revisited

Checkpoints

A checkpoint is a \((block, slot, slot)\) triple \((B,c,p)\) where \(p = slot(B)\), and \(c\) is the slot in which \(B\) is proposed for justification (corresponding to the epoch in Casper-FFG checkpoints). Other than for the genesis checkpoint \((G,0,0)\), we always have \(c > p\). We refer to \(p\) as the proposal slot of \(B\) and to \(c\) as the checkpoint slot of \((B,c,p)\).

FFG vote

An FFG vote is a link \((B_1,c_1, p_1) \to (B_2, c_2, p_2)\) between a source and a target checkpoint, with \(B_1 \preceq B_2\) and \(c_2 > c_1\).

Justification

The genesis checkpoint \((G, 0, 0)\) is justified. Any other checkpoint \((B,c,p)\) is justified if there is a set of 2/3+ FFG votes \((A_i, c_i, p_i) \to (B_i,c, p_i')\), where \(A_i \preceq B \preceq B_i\) and all sources \((A_i, c_i, p_i)\) are justified. Note that the source and target blocks can be different across votes.

Finalization

A checkpoint \((B,c,p)\) is finalized if it is justified and there is a set of 2/3+ FFG votes with source \((B,c,p)\) and target slot \(c+1\), i.e. votes \((B,c,p) \to (B_i, c+1, p_i)\). In this case only target blocks are allowed to be different as the target checkpoint slot must be \(c+1\).

Greatest justified checkpoint and fork-choice root

Letting \((c_1, p_1) < (c_2, p_2)\) be defined by lexicographic ordering, we define an ordering on checkpoints by \((B_1,c_1,p_1) \prec (B_2,c_2, p_2)\) if \((c_1, p_1) < (c_2, p_2)\). We often consider the greatest justified checkpoint, defined with respect to this order. If the greatest justified checkpoint is \((B,c,p)\) we refer to \(B\) as the fork-choice root.

The figure shows all justified checkpoints after 4 slots. From left to right, the checkpoint slot increases, and for a given checkpoint slot the the proposal slot decreases top to bottom. Here we assume that all justifications happen through votes that have the same source and target, indicated through the arrows. Blocks \(A,B,C,D\) are proposed at slot \(0,1,2,3\), respectively. At slot \(2\), votes with source \((A,1,0)\) and target \((B,2,1)\) justify both \((B,2,1)\) and \((A,2,0)\). Nothing is justified at slot \(3\), while at slot \(4\) checkpoints with blocks \(B,C,D\) are justified, by votes with source \((B,2,1)\) and target \((D,4,3)\). At this point, \((D,4,3)\) is the greatest justified checkpoint.

Note that the greatest justified checkpoint is very much related to the latest justified checkpoint in plain Casper-FFG (epoch vs slot terminology aside). The lexicographic ordering first considers the checkpoint slot \(c\), restricting our choice to justified checkpoints of latest checkpoint slot, which in Casper-FFG would already yield a unique checkpoint, precisely the latest justified. Instead, here it is possible to have multiple justified checkpoints with the same checkpoint slot, and we may need the extra step of choosing the one with the greatest proposal slot \(p\) among those, as per the ordering.

Slashing

Two different votes \((B_1,c_1, p_1) \to (B_2, c_2, p_2)\), \((B_1', c'_1, p'_1) \to (B_2', c'_2, p'_2)\) are slashable if:

• Equivocation: \(c_2 = c_2'\) (two different votes for the same checkpoint slot)
• Surround voting: \((c_1', p_1') < (c_1, p_1)\) and \(c_2 < c'_2\) (a vote from a later slot uses a lower checkpoint as source)

Slashing can always be avoided by locally ensuring monotonicity of the greatest justified checkpoint, since this is what is used as the source of FFG votes (as in Casper-FFG, as we’ll see), i.e., only updating when receiving a new justified checkpoint which is greater with respect to \(\prec\).

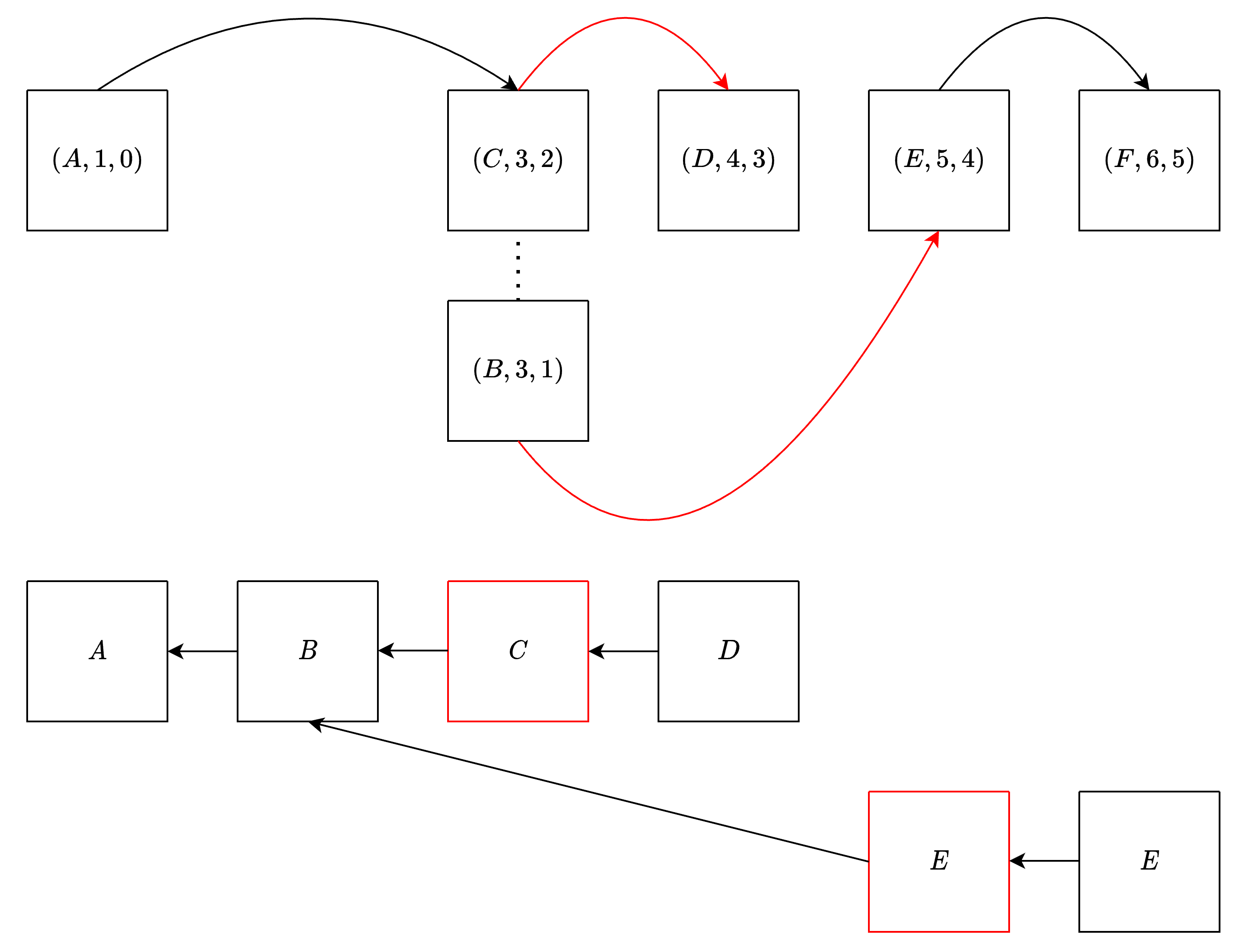
The figure depicts an instance of surround voting on top, with the slashable votes in red, and the fork corresponding to it on the bottom, with finalized checkpoints in red. From slot 4 to slot 3, the source has been moved “back” from checkpoint \((C,3,2)\) to the lower checkpoint \((B,3,1)\). This is in particular a case of surround voting that’s unique to this protocol and not present in Casper-FFG, because the two source checkpoints have the same checkpoint slot. Due to this, \((C,3,2)\) is finalized but \((E,5,4)\), a greater conflicting checkpoint, is justified and then finalized.

Fork-choice and confirmation

Attestations

An attestation is a head vote and FFG vote pair, where a head vote is just a (reference to a) block. Each attestation has a slot associated to it, which is the slot in which it should be sent, and corresponds to the checkpoint slot of the FFG vote target it contains.

Fork-choice

At any time a node can run the fork choice by starting from the fork-choice root then running the RLMD-GHOST. The output is the canonical chain, and the tip of the canonical chain is the chain head. A block is canonical if part of the canonical chain.

Confirmation candidates

A node keeps a set of blocks which we refer to as confirmation candidates. In slot \(p\) a node adds a block \(B\) to its set of confirmation candidates if at time \(2\Delta\) into the slot it has 2/3+ head votes from slot \(p\) that are in the subtree rooted at \(B\).

Confirmation

At any given time, a node considers a block \(B\) confirmed if either \(B\) is the fork-choice root or \(B\) is a canonical confirmation candidate. Note that the fork-choice root is canonical by definition, so all confirmed blocks are canonical. Moreover, each node always knows of a unique highest confirmed block, since the fork-choice root is always confirmed and confirmed blocks do not conflict because they are all in the canonical chain.

Protocol

The structure at slot \(p\) is propose-attest-confirm-freeze:

• time \(0\Delta\): The proposer runs the fork-choice and proposes a block extending its output, together with a view-merge message, containing the greatest justified checkpoint as well.
• time \(1\Delta\): Attesters do merging if necessary, run the fork-choice, and attest. An attesters will attest to \((B, \mathcal{J} \to \mathcal{T})\) where \(B\) is head of the chain, \(\mathcal{J}\) is the greatest justified checkpoint and \(\mathcal{T}\) is the target checkpoint, defined by \(\mathcal{T} = (C,p,slot(C))\) where \(C\) is the highest confirmed block.
• time \(2\Delta\): Attestations from slot \(p\) are used to identify new confirmation candidates.
• time \(3\Delta\): The view is frozen for view-merge.

Security analysis

Liveness theorem

Assume 2/3+ of the validators are honest and that the network is synchronous. If the proposer of slot \(t\) is honest and proposes block \(B\) then:

• confirmation: \(B\) is confirmed by all honest validators in slot \(t\)
• justification: \(\mathcal{T} = (B,t+1,t)\) is justified by all honest validators in slot \(t+1\)
• finalization: \(\mathcal{T} = (B,t+1,t)\) is finalized by all honest validators in slot \(t+2\)

Proof:

• confirmation: Let the greatest justified checkpoint in the proposer’s view be \(\mathcal{J} = (A,c,slot(A))\). Since \(A\) is the fork-choice root, \(A \prec B\). By view-merge, since the proposer of slot \(t\) is honest, all honest validators in slot \(t\) attest to head \(B\). By time \(2\Delta\), honest validators have received the 2/3+ honest attestations with head vote \(B\), so they mark \(B\) as a confirmation candidate. Since all honest validators (and nodes) also see \(B\) as canonical, they in particular consider \(B\) to be confirmed at this point.
• justification: Also by view-merge, all 2/3+ honest attestations from slot \(t\) have the same source \(\mathcal{J}\), though possibly different targets \((B_i, t, slot(B_i))\), all satisfying \(A \prec B_i\). Therefore, the checkpoint \((A, t, slot(A))\) is justified by all honest validators. In slot \(t+1\), the greatest justified checkpoint seen by any honest validator must then have checkpoint slot \(t\), since at least one such justified checkpoint exists and \(t\) is the latest slot. Justified checkpoints with checkpoint slot \(t\) and higher proposal slot than \(slot(A)\) could exist, and would be greater than \((A,t,slot(A))\), but crucially we are going to show that the associated blocks can only be ancestors of \(B\). If that’s the case, the greatest justified checkpoint since by an honest validator in slot \(t+1\) would necessarily have an ancestor of \(B\) as its block, and thus the fork-choice root of any honest validator at slot \(t+1\) would be an ancestor of \(B\). To show this, note that \(B_i\) is seen as confirmed by the validator sending the FFG vote with target block \(B_i\), and thus it is also seen as canonical by it. Since at the same time the validator also sees \(B\) as the head of the canonical chain, it follows that \(B_i \prec B\). Indeed, any checkpoint justified at slot \(t\) must be an ancestor of \(B\).
  An honest validator at slot \(t+1\) then attests with source \((B', t, slot(B'))\), where \(B' \prec B\). Moreover, it sees \(B\) as canonical, since the fork-choice root \(B'\) is an ancestor of \(B\) and is \(B\) is supported by all latest honest votes (those from slot \(t\)), which are a majority. Since \(B\) is a canonical confirmation candidate, the validator still sees it confirmed. It is then in particular the highest confirmed block, since a block from slot \(t+1\) could not already be a confirmation candidate. Therefore, all honest validators attest with target \(\mathcal{T}\), and \(\mathcal{T}\) is justified.
• finalization: In slot \(t+2\), \(t+1\) and \(t\) are the highest possible checkpoint and proposal slots that a justified checkpoint could have, so \(\mathcal{T}\) is the greatest justified checkpoint for all honest validators. Therefore, they all cast FFG votes with source \(\mathcal{T}\), resulting in its finalization.

Accountability

Proof: Let \((B,c, p)\) be finalized at slot \(t+1\). We assume that no checkpoint \((B',c, p')\) with \(B'\) conflicting with \(B\) is justified at slot \(c\), as that would clearly involve 1/3+ equivocation, because the votes which count for justification of \((B,c,p)\) must have target blocks in the subtree of \(B\) and the votes which count for justification of \((B',c, p')\) must have target blocks in the subtree of \(B'\), and these two subtrees are disjoint by assumption. Then, suppose \(c'\) is the smallest slot \(> c\) such that a checkpoint \((B', c', p')\) is justified and \(B \not \preceq B'\), i.e., either \(B'\) conflicts with \(B\) or it is a strict ancestor of it. Here we assume that one such slot exists, and argue by contradiction. Consider a vote \((A_i, c_i, p_i) \to (B_i, c', p_i)\) involved in the justification of \((B', c', p')\), by a validator which has also voted for \((B,c, p) \to (*, c+1)\), i.e. to finalize \((B,c, p)\). By definition of justification, \(A_i \preceq B' \preceq B_i\). There are a few cases:

• \(c' = c + 1\). Then two sub-cases:
  • If \(B'\) conflicts with \(B\), the validator is slashable for equivocation because \(A_i \preceq B'\) implies \(A_i \neq B\), and thus the two votes are different.
  • If \(B'\) is a strict ancestor of \(B\), i.e., \(B' \precneqq B\), then we have \(A_i \preceq B' \precneqq B\), and thus \(A_i \neq B\). Again, the validator is slashable for equivocation.
• \(c' > c + 1\). Three sub-cases:
  • \(c_i < c\): we have the “normal case” of surround voting, because \(c_i < c < c+1 < c'\). In our surround voting notation, \((c_i, p_i) < (c, p)\) and \(c+1 < c'\).
  • \(c_i = c\): by the initial assumption, there is no justified checkpoint conflicting with \(B\) with checkpoint slot \(c\), so \(A_i\) does not conflict with \(B\). Two more cases:
    • \(B \preceq A_i\): then also \(B \preceq A_i \preceq B'\), contradicting the assumption that \(B \not \preceq B'\). In other words, \((B', c', p')\) is a harmless justification, compatible with \((B, c, p)\).
    • \(A_i \precneqq B\): then \(p_i = slot(A_i) < slot(B) = p\), so we have surround voting, because \((c_i, p_i) = (c, p_i) < (c, p)\) and \(c+1 < c'\).
  • \(c_i > c\): \(c < c_i < c'\) and minimality of \(c'\) imply that \(B \preceq A_i\), so also \(B \preceq B'\), again contradiction.

Rationale

• In an FFG vote \((A,s) \to (B,t)\), including the source \((A,s)\) serves two purposes at once:
  • Acknowledgment of a justification, leading to finality: firstly, the validators sending this vote acknowledge that at slot \(t\) they know that the checkpoint \((A,s)\) is justified, and thus commit to never trying to justify a conflicting checkpoint, unless they first observe a later conflicting one, which justifies their switching away from the subtree of \(A\). This is in particular helpful if \(s = t-1\), as 2/3+ such votes lead to finality. This has nothing to do with \(B\), and we could replace the whole vote \((A,t-1) \to (B,t)\) with \((A,t-1,t)\) without affecting finality at all. In fact, this is essentially what we do when modifying the definition of finality to allow for different target blocks. Note that this is the same purpose of a pre-commit vote in Tendermint, or a commit in PBFT, i.e., an acknowledgment that a 2/3+ quorum has been observed.
  • Automatic tracking of the root cause of double finality: double finality happens when 1/3+ of the validators unjustifiably ignore a commitment they made, i.e., when they vote to justify a target which conflicts with a previously acknowledged justified checkpoint, without there being any earlier instance of such a conflicting justified checkpoint. In Tendermint, this corresponds to validators ignoring the “pre-vote the lock” rule: validators have sent a pre-commit for \(B\), but then unjustifiably unlock, i.e., they pre-vote something else without having seen a proof-of-lock-change (a later quorum of pre-votes for something other than \(B\)). In Tendermint, unlocking can lead to slashing only if someone is asked for justification, i.e, for a proof-of-lock-change which would explain the unlock, and fails to provide it. In Casper-FFG, asking for proof is not necessary, precisely because of FFG votes including a source, which is required to be itself justified. If a validator acknowledges that \((B,t)\) is justified and later wants to “unlock”, i.e., attempt to justify some checkpoint \((A,t')\) with \(t' > t\) and \(B \not \preceq A\), it needs to send an FFG vote with target \((A,t')\) and with a justified source. If the unlock is unjustifiable, i.e., there is at this point no justified checkpoint conflicting with \(B\) and later than \(B\), the FFG vote will necessarily need to use an earlier source, i.e. doing surround voting, so that the fault can be directly detected. This has the same effect to modifying Tendermint so that pre-votes come with a proof-of-lock-change already, which essentially prevents having to ask for justification by forcing it to be provided upfront. With all this in mind, it should be clear that this purpose is not harmed by allowing the votes contributing to a justification to have different sources, as long as they are all themselves justified: each vote should come with its own evidence, but the evidence does not need to be exactly the same for all votes, it just needs to be verifiable for each.
• As already mentioned, the target \((B,t)\) of an FFG vote corresponds to a pre-vote in Tendermint, or a prepare in PBFT, i.e., it marks \(B\) as a candidate lock. The key thing to ensure here is that \(B\) does not conflict with something that people are already locked on, since this could otherwise cause a safety violation, hence why \(B\) needs to be a descendant of the latest justified block, i.e., the only lock we have to worry about (as it itself unlocks all earlier locks). Another subtlety due to this being an ebb-and-flow protocol is that validators also need to restrict their targets to confirmed blocks. A vote \((A_i, s_i) \to (B_i, t)\) with \(A_i \preceq B \preceq B_i\) then indicates \(B\) as a suitable candidate lock in the view of its sender, because \(A_i \preceq B\) means that it sees \(B\) as a descendant of the latest justified and \(B \preceq B_i\) means that it sees it an ancestor of a confirmed block, and thus itself confirmed.