# Retrospective Roadmap: Navigating Through a Year of Theoretical Consensus Research #### [Luca Zanolini](https://twitter.com/luca_zanolini) Over the last year, our theoretical research has been primarily focused on developing consensus protocols that can be seen as building blocks to achieve *single slot finality* [^1](https://notes.ethereum.org/@vbuterin/single_slot_finality) within Ethereum. This means the protocols are designed to finalize a block within the same slot it is proposed. We have drawn inspiration from the *ebb-and-flow* paradigm described by Neu, Tas, and Tse[^2](https://arxiv.org/abs/2009.04987), which balances two interlocking components. The first is a synchronous consensus protocol, known as the *dynamically available component*, responsible for reaching agreement in case of fluctuation in the participation level of validators. The second is a partially synchronous protocol, referred to as the *finalizing component* (or *gadget*). This component finalizes the blocks output by the available component and ensures their safety during periods when the network's communication is asynchronous. Our exploration has been particularly deep into the mechanisms of the dynamically available component, aiming to optimize its efficiency and reliability. To achieve this, we systematically explored different approaches to devising not only effective but also secure dynamically available protocols. In the following sections, we summarize our research efforts that have thus far been documented and shared through scientific papers. ## RLMD-GHOST In one of our initial studies, we examined the theoretical constraints of Gasper[^3](https://notes.ethereum.org/@luca-zanolini/SyZAX6V8o), the consensus protocol currently in use by Ethereum. Specifically, we focused on the limitations within LMD-GHOST, which serves as Gasper's dynamic available component. While the Goldfish protocol[^4](https://arxiv.org/abs/2209.03255) has partially addressed these issues, it has not resolved them fully. Our focus has particularly been on the challenges that arise during unpredictable periods of network asynchrony. A notable limitation of dynamically available consensus protocols is their inability to tolerate network partitions[^5](https://arxiv.org/abs/2006.10698). No consensus protocol can simultaneously satisfy liveness (under dynamic participation) and safety (under temporary network partitions, or temporary asynchrony). In other words, it is impossible for a consensus protocol (for state-machine replication) to output a single chain, while simultaneously offering dynamic availability and ensuring transaction finality, even during asynchronous periods or network partitions. For this reason, dynamically available protocols are devised assuming a synchronous network. In [Recent Latest Message Driven GHOST: Balancing Dynamic Availability With Asynchrony Resilience](https://arxiv.org/abs/2302.11326) (to appear in [CSF 2024](https://www.ieee-security.org/TC/CSF2024/)), we present RLMD-GHOST, a synchronous dynamicaly available consensus protocol that maintains safety during *bounded* periods of asynchrony and that generalizes both LMD-GHOST and Goldfish. Although it respects the known limits of dynamically available consensus protocols -- thus not violating the aforementioned impossibility result -- it provides some level of assurance when faced with short-lived asynchrony during protocol executions. RLMD-GHOST proceeds in slots consisting of $4\Delta$ seconds, each having a proposer $v_p$, chosen through a proposer selection mechanism among the set of validators. In particular, at the beginning of each slot $t$, the proposer $v_p$ proposes a block $B$. Then, all active validators vote after $\Delta$ seconds for a block (optimistically for $B$), after having merged their *view* -- a set containing the messages they received (at some point during the execution) -- with the view of the proposer. RLMD-GHOST is characterized by a fork-choice function -- a deterministic function that takes as input the view of a validator $v_i$ and it locally outputs to $v_i$ a *canonical chain* -- which is used by honest proposers and voters to decide how to propose and vote, respectively, based on their view while performing those actions. In particular, the fork-choice function we have developed takes into account only the most recent messages from validators, specifically those that are not considered equivocating and that have been sent within a time frame not exceeding $t-\eta$ slots. This function operates as follows to determine the canonical chain for a validator $v_i$ at slot $t$: - It begins with the local view of validator $v_i$. - The genesis block serves as the initial point for constructing the canonical chain. - The function then sequentially selects the next block in the chain by identifying the child block that anchors the heaviest subtree. This is assessed based on the cumulative stake of the most recent, non-equivocating votes for its descendants, again considering only those votes cast within the latest $t-\eta$ slots. In particular, in a given slot $t$, the designated proposer evaluates the fork-choice function to identify the current tip of the canonical chain. Upon determining this, the proposer attaches a new block to the tip and disseminates this block, together with their view, to the rest of the validators. Upon receipt, each validator merges their own local view with that of the proposer, and executes the fork-choice function based on this new view. The outcome is a vote cast by each validator for the chain’s tip—which, under optimal conditions, aligns with the block proposed by the proposer. RLMD-GHOST results in a synchronous protocol that has interesting practical properties. It is dynamically available and reorg resilient in (a generalization of) the sleepy model[^6](https://eprint.iacr.org/2016/918.pdf). This generalization is weaker than the usual sleepy model, because of some extra assumptions on the adversary, not allowing for fully variable participation. However, RLMD-GHOST results resilient to asynchronous periods lasting less than $\eta -1$ slots, meaning that honest proposals made before the period of asynchrony are still canonical after it. In other words, we are trading off allowing fully variable participation for more resilience to temporary asynchrony, which we think is a very sensible tradeoff in practice. Some explanations of RLMD-GHOST can be found [in this talk given at SBC 2023](https://www.youtube.com/watch?v=Nx5bgyJ7SJ4&t=4780s) and [in this talk given at a16zcrypto](https://www.youtube.com/watch?v=F2olypDSVnA). The RLMD-GHOST protocol, as it stands, faces certain practical constraints, notably the necessity for the entire validator set to cast votes in each slot. Considering the existing number of validators in Ethereum[^7](https://beaconcha.in/validators), implementing this protocol efficiently presents a challenge. Further research is required to investigate advanced signature aggregation schemes or alternative methods to alleviate this limitation. Nevertheless, the techniques employed in this work that confer resistance to bounded periods of asynchrony have broader applications. As we will discuss in subsequent sections, these techniques can be adapted to enhance other dynamically available consensus protocols as well. ## A simple single slot finality protocol for Ethereum With the foundation of a dynamically available consensus protocol like RLMD-GHOST, the transition to a single slot finality protocol is quite straightforward. Specifically, we have devised a [Simple Single Slot Finality protocol for Ethereum](https://arxiv.org/abs/2302.12745) (published at [CBT 2023](https://deic.uab.cat/cbt/cbt2023/) within [ESORICS](https://esorics2023.org)) as a secure ebb-and-flow protocol using a *confirm-finalize* method. This method stipulates that for blocks to be finalized, they must first be confirmed by the underlying dynamically available consensus protocol. In practice, this means that honest validators would not vote to finalize a block which they do not see as confirmed. In conditions where the network is synchronous, the finality gadget operates without compromising the dynamically available protocol's output chain, thereby preserving its designed security properties. Consequently, the overall ebb-and-flow protocol retains dynamic availability as long as the base available protocol, i.e., RLMD-GHOST in our case, does. An essential attribute of RLMD-GHOST is its capability for what we call *fast confirmations*. This ensure that honest block proposals get confirmed within their respective proposal slot, assuming that a supermajority of at least two-thirds of the honest validators are online and active. This fast confirmation process is vital for achieving single slot finality, as it enables the immediate justification and finalization of these swiftly confirmed honest proposals. Similarly to Gasper, our protocol employs a justification-respecting hybrid fork-choice function, in this case based on RLMD-GHOST. Such fork-choice function starts from the latest justified block, and then runs the fork-choice function implemented in RLMD-GHOST (quickly described in the section above) from there. Our protocol proceeds in slots, each one having a single proposer, and involves two types of votes, head-votes, which are relevant to the dynamically available protocol (RLMD-GHOST) and FFG-votes, to justify and finalize. This results in two rounds of voting for each slot. - A proposal $B$ is made by the proposer of a given slot $t$. - Head-votes are cast for the tip of the canonical chain, i.e., the chain determined by the fork-choice function executed at slot $t$. - Validators use the head votes from the current slot to fast confirm some block, the highest one whose subtree has received votes from $2/3$ of the validator set, if any. Optimistically, the current proposal $B$ is immediately fast confirmed. - FFG-votes are cast. Optimistically, the current proposal is justified. - Validators *acknowledge* the justification of slot $t$. If $2/3$ of the validators cast an acknowledgment for the same block $B$, $B$ gets finalized within slot $t$.  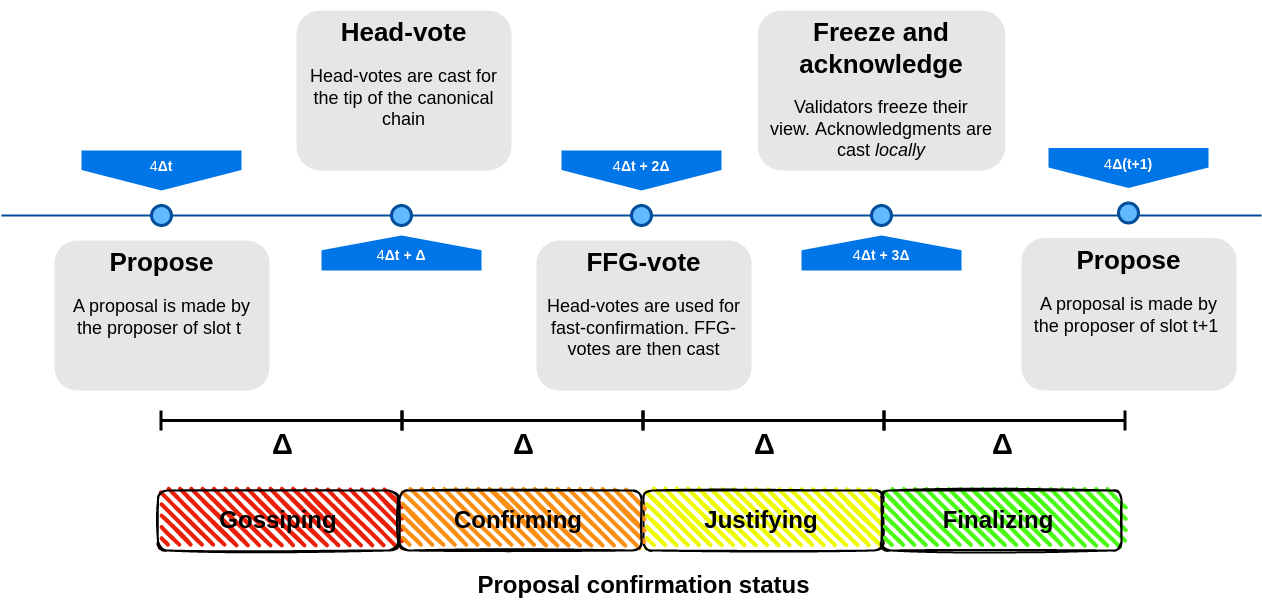An overview of this protocol can be found [in this ethresear.ch blog post](https://ethresear.ch/t/a-simple-single-slot-finality-protocol/14920). ## Dynamically available consensus with single-vote decisions in the sleepy model Our research continued beyond the initial heaviest-chain protocols like RLMD-GHOST, Goldfish, and LMD-GHOST -- all of which derive their functioning from a fork-choice function that tallies votes without any built-in quorum-based configuration. We then shifted focus to a different paradigm within the realm of dynamically available consensus protocols -- those that employ a quorum-based approach ensuring safety deterministically. These protocols are designed around a predetermined quorum system, with their security guarantees depending on quorum intersection and quorum availability. In networks with dynamic participation, these quorum systems necessitate novel techniques for the formulation of *quorum certificates* (commonly represented as "$f+1$ votes for the same value" in static models) and *certificate transferability*. The reason for that is due to the fact that different participants might have different perception about the participation level at a specific point in the execution. To address these challenges, cutting-edge solutions have been introduced, such as the *time-shifted quorum technique* [^8](https://eprint.iacr.org/2022/404) , which enables the transferability of quorum certificates within networks with dynamic participation. Exemplifying this class are protocols such as the one introduced by Momose and Ren[^9](https://eprint.iacr.org/2022/404) (CCS 2022), the protocol by Gafni and Losa[^10](https://arxiv.org/pdf/2301.04817.pdf) (DISC 2023), and the Malkhi, Momose, and Ren protocol[^11](https://eprint.iacr.org/2022/1448) ([CCS 2023](https://www.sigsac.org/ccs/CCS2023/)). 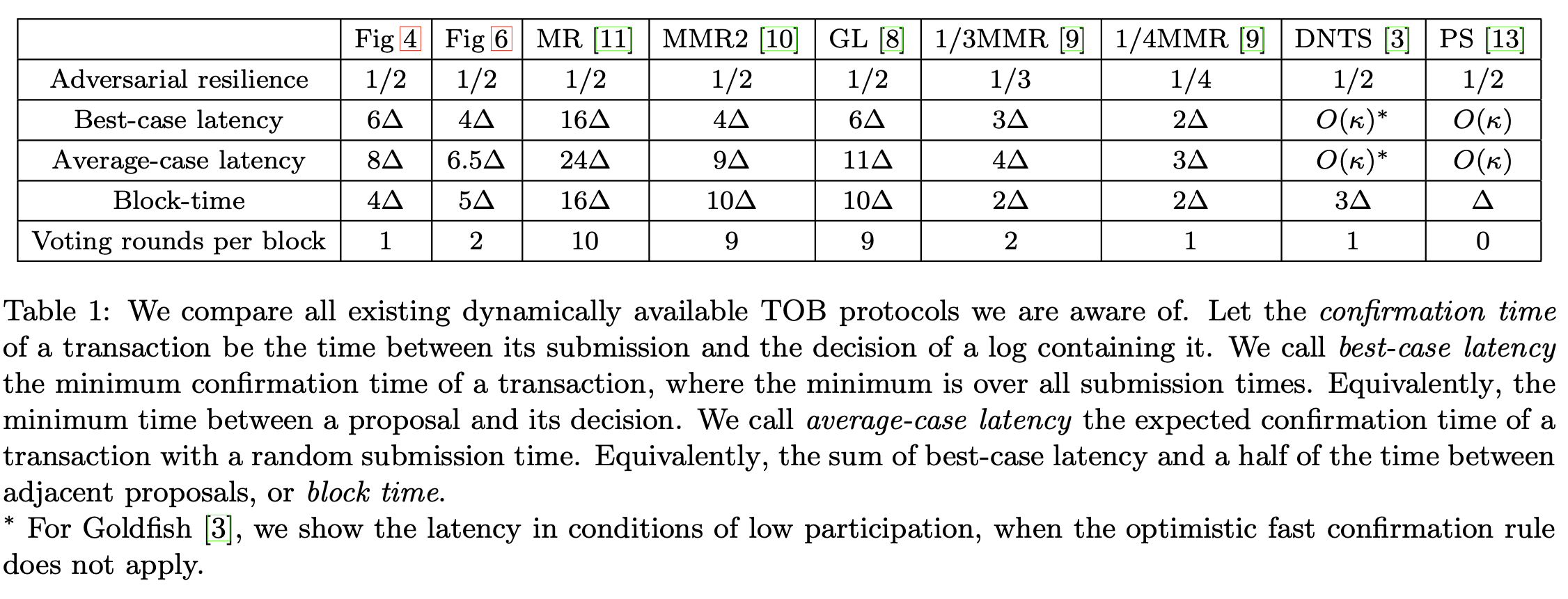A common pattern in the structure of these quorum-based consensus protocol is that they all leverage a *Graded Agreement*[^12](https://arxiv.org/abs/2308.04646) (GA) primitive, albeit with different implementations and properties. In this primitive, each participant starts with an initial input value. The protocol is designed so that honest participants eventually output values assigned with a specific *grade*. Commonly, implementations use a grading system with two levels: 0 and 1. However, some variants of this primitive extend the grading system to include a third level, grade 2. The currently existing dynamically available consensus protocols with optimal adversarial resilience and latency constant in the security parameter, i.e., [9-10-11 right above] all share the drawback of requiring multiple rounds of voting for each decision. In practice, these protocols all operate in views, and within each view a block is proposed and a decision is made. To do so, [two](https://arxiv.org/pdf/2301.04817.pdf), [three](https://www.sigsac.org/ccs/CCS2023/), and [five](https://eprint.iacr.org/2022/404) instances of Graded Agreement are invoked within a view, each including four, three, and two rounds of voting, respectively. This hinders their practicality in real-world systems where a large number of participants are involved simultaneously, as is the case in the Ethereum blockchain, because voting rounds can be quite slow and expensive in such systems. In [Streamlining Sleepy Consensus: Total-Order Broadcast with Single-Vote Decisions in the Sleepy Model](https://arxiv.org/abs/2310.11331) we extend this line of work, with the aim of improving the practicality of quorum-based dynamically available consensus protocols, in particular for systems with a large number of participants. We introduce a consensus protocol that tolerates up to $1/2$ adversarial participants, has comparable latency to the [state-of-the-art](https://www.sigsac.org/ccs/CCS2023/) in this respect, and only necessitates a single instance of Graded Agreement, and a single voting round, per view. To do so, we devise a three-grade Graded Agreement primitive with appealing properties, such as uniqueness of outputs of any grade. In particular, we build this primitive upon the Graded Agreement primitive introduced by Momose and Ren, and we adopt a variant of the time-shifted quorum technique that also handles equivocations of inputs.  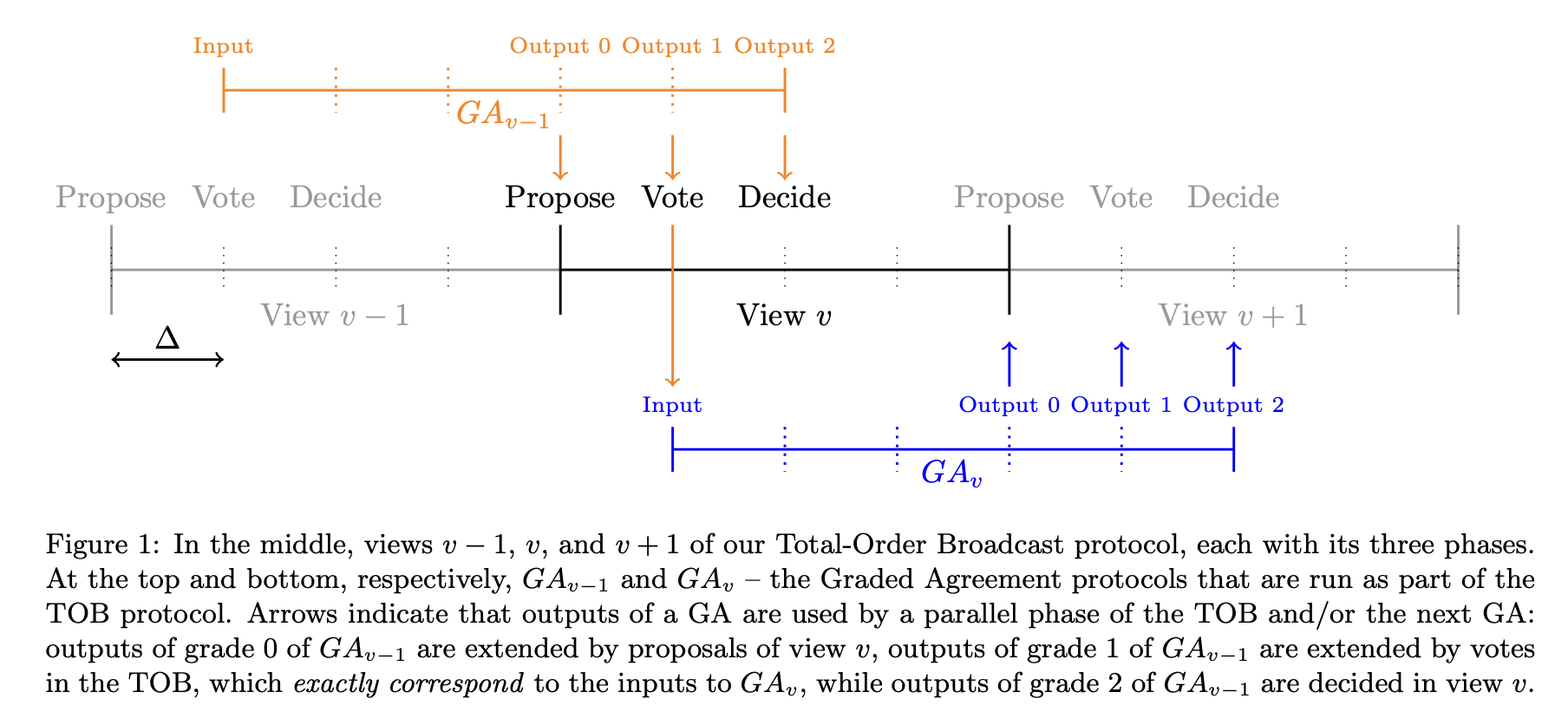Given such Graded Agreement, we devised a dynamically available consensus protocol (or, to be precise, a Total-Order Broadcast TOB protocol.) Specifically, our TOB protocol proceeds over a series of views, each spanning a duration of $4\Delta$. Every view $v$ initiates a Graded Agreement $GA_v$ with grades $0$, $1$, and $2$, which extends and overlaps with the following $GA_{v+1}$ during view $v+1$. This structure implies that a single view doesn't encapsulate a full cycle of a Graded Agreement; instead, a $GA_v$ initiated in view $v$ concludes its operations only in the succeeding view $v+1$. At a high level, our protocol operates through the following phases. - **Proposal Phase**: This phase corresponds to the grade $0$ output phase of $GA_{v-1}$. Validators propose a log extending their *candidate* log, the grade $0$ output from $GA_{v-1}$. - **Voting Phase**: This phase corresponds to both the input stage of $GA_v$ and the grade $1$ output phase of $GA_{v-1}$. Validators with a grade $1$ output treat it as a *lock*. To maintain safety, they only input to $GA_v$ either the lock or a proposal that extends it. - **Decision Phase**: This phase corresponds to the grade $2$ output phase of $GA_{v-1}$. Validators *decide* their grade $2$ output.  In the table below, our protocol is referred to as Fig.4. Moreover, we have [MR](https://eprint.iacr.org/2022/404), [MMR2](https://www.sigsac.org/ccs/CCS2023/), [GL](https://arxiv.org/pdf/2301.04817.pdf), which are Momose and Ren (MR), Malkhi, Momose, and Ren (MMR2), and Gafni and Losa (GL), respectively. Observe that DNTS and PS are not quorum-based protocols.  ## Improving asynchrony resilience in quorum-based consensus protocols However, due to the impossibility result mentioned few sections above, such quorum-based dynamically available consensus protocols must assume network synchrony as well and they lose their safety guarantees during arbitrarily long periods of asynchrony. In [Improving Asynchrony Resilience in Dynamically Available Total-Order Broadcast Protocols](https://arxiv.org/abs/2309.05347), we explore the challenge of tolerating bounded periods of asynchrony in quorum-based dynamically available protocols. We propose to trade off assumptions limiting the online/offline churn rate in exchange for tolerating bounded asynchronous periods through the use of a configurable message-expiration period. This is aligned with the techniques introduced with the RLMD-GHOST protocol. We show how to apply this idea to a state-of-the-art protocol[^13](https://eprint.iacr.org/archive/2022/1448/20230910:162058). This is a total-order broadcast protocol (1/3MMR, in Table 1) with adversarial resilience $1/3$ that builds upon a two-grade Graded Agreement primitive.  In particular, we extend such GA to make use of message expiry -- messages cast by participants have an expiration period of $\eta$ rounds (analogue of the $\eta$ parameter in the context of the RLMD-GHOST protocol), and only mesages cast within the latest $\eta$ rounds influence the protocol's behavior at a given round $r$. Such extension is not trivial, but it results in a GA that can tolerate bounded periods of asynchrony of duration $\eta - 1$. Based on this result, we extended the TOB protocol of Malkhi, Momose, and Ren (Algorithm 1) by replacing their GA with our extended one. The result is a dynamically available protocol that can tolerate bounded periods of asynchrony at the cost of a reduced adversarial resilience. Moreover, the techniques utilized in this work can be directly applied to other deterministically safe, dynamically available consensus protocols. As highlighted at the beginning of this post, our primary focus here has been on research related to single slot finality, a theme that has been central to our efforts over the past year. We have presented four key works that encapsulate our progress in this area. However, it's important to note that our research extends beyond this singular focus. For those interested in a broader view of our work, I encourage you to visit our [website](https://ethconsensustalks.com), where you can explore the full spectrum of our research and its various dimensions.