# Evolution of the Ethereum Proof-of-Stake Consensus Protocol - Part II
###### [Luca Zanolini](https://twitter.com/luca_zanolini)
In this second part we analyze some of the most important problems faced by Gasper, and we present the current solutions that have been devised to cope with them. The first part, where we presented Gasper and its properties, can be found [here](https://notes.ethereum.org/GgixO3A1TrSBTfif1E8etw).
#### Disclaimer
Since this document only aims at grouping together all the most relevant resources concerning the proof-of-stake consensus protocol of Ethereum, some parts are just imported as they are in the original source. If this is the case, the text will be in *italic type* and the original reference is given.
#### Acknowledgments
Special thanks to Ittai Abraham, Aditya Asgaonkar, Francesco D'Amato, Tyler Holmes, Joachim Neu, and anonymous reviewers for feedback and helpful discussions.
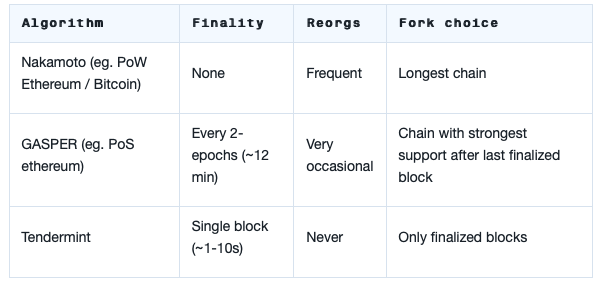
### Problems and Solutions
#### Problem: Balancing attack
[Neu *et al.*](https://arxiv.org/pdf/2009.04987.pdf) [https://ethresear.ch/t/a-balancing-attack-on-gasper-the-current-candidate-for-eth2s-beacon-chain/8079] have shown how the original version of Gasper, i.e., the one presented in the [first part](/GgixO3A1TrSBTfif1E8etw), suffers from a liveness issue that leads to loss of safety for the dynamically available ledger. They presented an attack against Gasper, called *balancing attack*, in the synchronous network model with adversarial network delay.
*Recall that Gasper proceeds in epochs which are further subdivided into $C$ slots each. For simplicity, let $C$ divide $n$ so that every slot has a committee of size $\frac{n}{C}$. For each epoch, a random permutation of all $n$ validators assigns validators to slots’ committees and designates a proposer per slot. Per slot, the proposer produces a new block extending the tip determined by the fork-choice rule $HLMD(G)$ executed in local view $G$. Then, each validator of the slot’s committee decides what block to vote for using $HLMD(G)$ in local view $G.$*
*For the Casper FFG layer, a block can only become finalized if two-thirds of validators vote for it. The attacker aims to keep honest validators split between two options (left and right chain) indefinitely, so that neither option ever gets two-thirds votes and thus no block ever gets finalized. Key technique to maintain this split is that some adversarial validators (‘swayers’) withhold their votes and release them only at specific times and to specific subsets of honest nodes in order to influence the fork-choice of honest nodes and thus steer which honest nodes vote left/right.* [https://arxiv.org/pdf/2009.04987.pdf]
The attacks requires an adversary to (i) know at what points in time honest validators execute HLMD-GHOST and (ii) be able to target a message for delivery to an honest validator just before a certain point in time. Moreover, it assumes that (iii) honest validators cannot *quickly* update each other about messages they have just received.
The adversary waits until the the proposer in the first slot of an epoch is Byzantine and there are at least six Byzantine validators in every slot of the epoch. Let us assume that this is the case in epoch $0$. The Byzantine proposer of slot $0$ *equivocates* and produces two conflicting blocks (left/blue and right/yellow) which it reveals to two suitably chosen equal-sized subsets of the committee. One subset votes left, the other subset votes ‘right’, obtaining a tie.
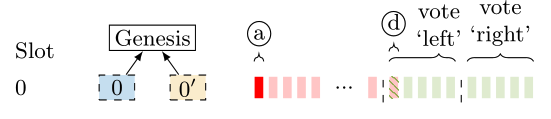
Observe that if the number of honest validator is not even, then the adversary recruits a Byzantine validator ($d$) to behave like an honest one. Finally, all blocks are delivered to every validator before $\Delta$. Note that the only Byzantine validators that cast a vote for slot $0$ are only $a$ and $d$.
At this point, the adversary selectively releases withheld votes (from Byzantine validators ($c$)) from slot $0$ to split validators of slot $1$ into two groups of equal size, one which sees left\blue as leading and votes for it, and one which sees right/yellow as leading and votes for it, reaching again a tie.
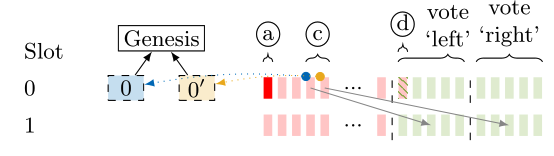
The adversary continues this strategy to maintain the tie throughout epoch $0$.
During epoch $1$, the adversary selectively releases additional withheld votes from epoch $0$ ($b$) to keep splitting validators into two groups, one of which sees left/blue as leading, the other sees right/yellow as leading, voting left/blue and right/yellow, respectively.
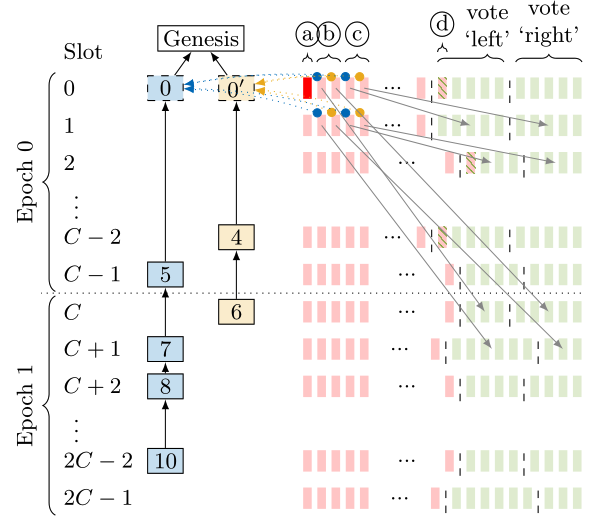
Finally, for epoch $2$ and beyond the adversary repeats its actions of epoch $1$. This continues indefinitely preventing finalization. Hence, Gasper is not secure in the synchronous model.
[comment]: # (Attacking Gasper without adversarial network delay)
#### (Part Of The) Solution: Proposer Weight Boosting
The balancing attack just presented is based on the fact that an attacker, by manipulating the network, can create a disagreement at the end of each slot regarding which messages count for the fork-choice, and therefore a disagreement on which chain is the winning chain.
[The proposed solution](https://notes.ethereum.org/@vbuterin/lmd_ghost_mitigation) to avoid the balancing attack is to increase the *attestation weight* of the proposer of a block in a given slot, if some conditions are met. In details, let us assume that all the attesters assigned to slot
$i$, i.e., validators in the committee that cast attestations in slot $i$, have collective total weight $W$. Then, the proposer in slot $i+1$ is expected to make a proposal immediately at the start of its slot. Its proposal implicitly chooses a particular chain. In this way, attesters of slot $i+1$, if they see the proposal arriving before $\frac{1}{3}$ of the way into a slot, they treat that proposal as equivalent to an attestation with weight $\frac{W}{4}$. Observe that this attestation weight for the proposer is valid only for slot $i+1$; after that, this weight is reverted.
:::spoiler
:::info
Proposer LMD Score Boosting: [https://github.com/ethereum/consensus-specs/pull/2730]
```python=
def on_block(store: Store, signed_block: SignedBeaconBlock) -> None:
...
# Add proposer score boost if the block is timely
time_into_slot = (store.time - store.genesis_time) % SECONDS_PER_SLOT
is_before_attesting_interval = time_into_slot < SECONDS_PER_SLOT // INTERVALS_PER_SLOT
if get_current_slot(store) == block.slot and is_before_attesting_interval:
store.proposer_boost_root = hash_tree_root(block)
...
```
Recall that `on_block` runs whenever a `SignedBeaconBlock` is received, updating the `store` for the fork-choice rule. In [Part I](/GgixO3A1TrSBTfif1E8etw) we define these objects.
:::
#### Problem: A Balancing Attack Despite Proposer Weight Boosting
Despite the proposer weight boosting solution presented above, [Neu *et al.*](https://arxiv.org/pdf/2203.01315.pdf) have shown that the LMD aspect of HLMD-GHOST still enables balancing attacks to Gasper.
LMD is devised as it follows. Every validator has a local table of the latest message that it received from each other validator, and that can be updated if some conditions are met. In particular, when a validator $v_i \in \mathcal{V}$ receives a valid message (i.e., a vote) from another validator $v_j \in \mathcal{V}$, then the latest message table entry for $v_j$ is updated if and only if new vote of $v_j$ is from a slot *strictly later* than the current latest message table entry. Thus, if $v_i$ observes two equivocating votes from $v_j$ for the same slot, validator $v_i$ considers the vote from $v_j$ received earlier in time. [https://ethresear.ch/t/balancing-attack-lmd-edition/11853]
We present the example showing the attack presented by Neu *at al.* Let $W=100$ be the number of total validators per slot and let us assume that the proposal weight is $W_p = 0.7 W = 70$. Moreover, let us assume a fraction of Byzantine validators of $20\%$, i.e., we assume $20$ Byzantine validators in each slot. Finally, the attack starts when there are five consecutive slots with Byzantine proposers.
During the first four slots the Byzantine proposers create two parallel chains of $4$ blocks each. These chains are initially kept private from the honest validators. The $20$ Byzantine validators vote on each of the $4$ blocks in each slot, i.e., they equivocate.
For the fifth slot, the adversary includes all equivocating votes for the left and the right chains into two distinct blocks and attaches these blocks on the left and right chains, respectively. Then, it releases the two equivocating blocks from the fifth slot in such a way that roughly half of the honest validators see the left block first (let us call $L$ that set of honest validators) and with it all the equivocating votes for the left chain; and half of the honest validators see the right block first (let us call $R$ that set of honest validators) and with it all the equivocating votes for the right chain.

Honest validators in $L$ and $R$ believe that their chain (left and right, respectively) has $80$ votes, while the other has $0$ (this because votes that arrive later are not considered, due to LMD).
If now we assume that slot $6$ has an honest validator $v_i \in L$, then $v_i$ proposes a block extending the left chain. The left chain gains a (temporary) proposal boost equivalent to $70$ votes (recall that we assumed $W_p = 0.7W$). Thus, validators belonging to $L$ see the left chain as leading with
$150$ votes and vote for it. Conversely, validators belonging to $R$ see the left chain with $70$ votes while the right chain with $80$ votes. Thus they vote for the right chain.
At the end of slot $6$, the proposer boost disappears. In the view of each honest validator, both chains gained roughly the same amount of votes, namely half of the honest validators’ votes. Assuming $|L|=|R|=40$, the proportion of votes between the left chain and the right chain is $120:40$ from the view of validators in $L$, and $40:120$ from the view of validators in $R$.
So, this repeats in subsequent slots, with the honest validators in $L$ and $R$ voting for the left and right chains, respectively.
It is worth noting that, by assumption, if a message is received by an honest validator, then this message will be received also by every other honest validator. This implies that honest validators in $L$ will receive all the messages that honest validators in $R$ received, and vice-versa. So, Byzantine validators that equivocate will eventually be slashed. However, this does not prevent the attack to be placed.
#### (Other Part Of The) Solution: Equivocation Discounting
*Equivocations are attributable faults, punishable by slashing a posteriori, but this does not prevent the attack vector a priori given that only one validator is required for it, and that there is no immediate recovery, because the same validator can continue producing equivocating attestations in subsequent slots as well.* [https://arxiv.org/pdf/2209.03255.pdf]
We present the notion of *equivocation discounting*, a solution to the attack presented in the section right above. On a high level, with equivocation discounting, we rely on every validator eventually recognizing equivocations and discarding them by stopping to give them weight. Formally, we require:
* **Fork-choice discounting**: When a validator $v_i$ runs HLMD-GHOST at slot $t$, it only counts votes from eligible validators $v_j$s for which the view of $v_i$ contains at most a single vote for each slot $v_j$s voted for, i.e., which are not viewed to have equivocated at previous slots.
In other words, we discard equivocating attestations from the fork-choice, and *discount*, i.e., do not consider the weight of, all future votes of equivocating validators for fork-choice purposes. Together with the LMD rule, the protocol considers only each validator’s most recent vote (or *attestation*) and, among them, only the non-equivocating ones.
Finally, observe that if a Byzantine validator $v_i$ equivocates, eventually every honest validator will have evidence that $v_i$ equivocated. This implies that, eventually, every equivocating validator $v_i$ will be *discovered* by every honest validator, and these equivocations will be used to slash $v_i$.
:::spoiler
:::info
Remove equivocating validators from fork-choice consideration: [https://github.com/ethereum/consensus-specs/pull/2845]
```python=
def on_attestation(store: Store, attestation: Attestation, is_from_block: bool=False) -> None:
...
# Update latest messages for attesting indices
update_latest_messages(store, indexed_attestation.attesting_indices, attestation)
```
with `update_latest_message` defined as
```python=
def update_latest_messages(store: Store, attesting_indices: Sequence[ValidatorIndex], attestation: Attestation) -> None:
target = attestation.data.target
beacon_block_root = attestation.data.beacon_block_root
non_equivocating_attesting_indices = [i for i in attesting_indices if i not in store.equivocating_indices]
for i in non_equivocating_attesting_indices:
if i not in store.latest_messages or target.epoch > store.latest_messages[i].epoch:
store.latest_messages[i] = LatestMessage(epoch=target.epoch, root=beacon_block_root)
```
```python=
def on_attester_slashing(store: Store, attester_slashing: AttesterSlashing) -> None:
"""
Run ``on_attester_slashing`` immediately upon receiving a new ``AttesterSlashing``
from either within a block or directly on the wire.
"""
attestation_1 = attester_slashing.attestation_1
attestation_2 = attester_slashing.attestation_2
assert is_slashable_attestation_data(attestation_1.data, attestation_2.data)
state = store.block_states[store.justified_checkpoint.root]
assert is_valid_indexed_attestation(state, attestation_1)
assert is_valid_indexed_attestation(state, attestation_2)
indices = set(attestation_1.attesting_indices).intersection(attestation_2.attesting_indices)
for index in indices:
store.equivocating_indices.add(index)
```
This function updates `store.equivocating_indices` with the validators that cast equivocating votes.
:::
#### Problem: Avalanche Attack (solved with equivocation discounting)
The [Avalanche Attack](https://arxiv.org/pdf/2203.01315.pdf) is an attack at proof-of-stake GHOST that combines selfish mining with equivocations [^7]. Observe that the attack exploits the fact that the weight of a block in GHOST is given by the number of ancestors that such block has. This differs from the *vote-based* variant of GHOST as used in PoS Ethereum, *where block weight is determined by votes and potentially a proposal boost*. [https://arxiv.org/pdf/2203.01315.pdf] However, a similar attack exists also in the vote-based paradigm. Finally, note that *only* [GHOST](https://eprint.iacr.org/2013/881.pdf) is considered, because its variant with LMD does not suffer from this attack.
[^7]: Observe that this attack is possible because of the assumed underlying proof-of-stake mechanism. Proof-of-work does not have equivocations.
*The adversary uses withheld blocks to displace an honest chain once it catches up in subtree weight with the number of withheld adversarial blocks. The withheld blocks are released in a flat but wide subtree, exploiting the fact that under the GHOST rule such a subtree can displace a long chain. Only two withheld blocks enter the canonical chain permanently, while the other withheld blocks can subsequently be reused (through equivocations) to build further subtrees to displace even more honest blocks. The attack exploits a specific weakness of the GHOST rule in combination with equivocations from PoS, namely that an adversary can reuse ‘uncle blocks’ in GHOST, and thus such equivocations contribute to the weight of multiple ancestors. Formal security proof of PoS GHOST seems doomed.* https://ethresear.ch/t/avalanche-attack-on-proof-of-stake-ghost/11854
We present the example showing the attack presented by Neu *at al.* Let us assume that the adversary starts with $k=6$ withheld blocks and does not gain any new blocks during the attack, meaning that the attack eventually stops. Observe that the larger the number of blocks that are withheld, the longer will the attack last.
First, the adversary withholds its subtree of $k=6$ withheld blocks, while honest nodes produce a chain. (In the figure below, red blocks are blocks from the adversary, while the green blocks constitute the honest chain.)

Once honest nodes reach a chain of length $6$, the adversary releases the withheld blocks. Observe that the main chain according to GHOST changes.

Note that the adversary can reuse blocks $3,4,5$ and $6$, in the form of equivocations, on top of the chain $B_{\text{genesis}} → 1 → 2$ formed by the first two withheld adversarial blocks, which is now the chain adopted by honest nodes. Again, once that new chain reaches length $4$, the adversary releases another subtree and, according to GHOST, the main chain changes again. Once the new chain reaches length $2$, the adversary releases the last displacing subtree.
Honest nodes now build on $6 \rightarrow 5 \rightarrow 4 \rightarrow 3 \rightarrow 2 \rightarrow 1 \rightarrow B_{\text{genesis}}$. All honest nodes so far have been displaced.

Observe that, through equivocation discounting, this attack can no longer be placed. Equivocating blocks are not considered during the fork-choice.
#### Problem: Ex-Ante Reorg
A reorg is an event where a block that was part of the canonical chain becomes no longer part of the canonical chain because a competing block beat it out. Reorgs can occur naturally due to network latency (also called *short reorgs*), or maliciously. In the first case, let us consider for example the proof-of-work. Here, if two miners create blocks $A$ and $A'$ at nearly the same time, then the network partitions with some honest nodes mining on top of $A$ and some mining on top of $A'$. If a new block $B$ is mined as a child of $A$ before any blocks are mined as a child of $A'$, then the network will see $A$ as the tip of the chain, making $A'$ *orphaned*. Every honest miner who saw $A'$ as the tip of the chain, switches to $A$ and deletes block $A'$ from the canonical chain.
The maliciously occurrency of reorgs are instead caused by an adversary who seeks to exploit reorgs for its own gain. This enables attacks like double-spending or front-running.
Reorgs can be classified in two categories: *ex post reorgs*, i.e., an adversary observes a block which subsequently attempts to fork out, and *ex ante reorgs*, i.e., an adversary attempts to fork out a future block that is unknown to the adversary at the start of the attack.
*Finality is a situation where a fork-choice rule so strongly favors a block that it is mathematically impossible, or economically infeasible for that block to get reorged. In some fork-choice rules, reorgs cannot happen; the fork-choice rule simply extends the existing chain by appending any blocks that have been finalized through consensus. In other fork-choice rules, reorgs are very frequent.* [https://www.paradigm.xyz/2021/07/ethereum-reorgs-after-the-merge]
With Gasper, *long reorgs*, i.e., reorgs that aim to fork out several blocks, are not possible because all blocks that are deeper than $2$ epochs in the past are considered finalized (see FFG Casper and Gasper sections). Moreover, ex post reorgs become practically impossible because an adversary controlling only a few validators has no way to beat the honest majority of thousands of attesters[^12]. In other terms, making a reorg directly requires the attacker to control close to $50\%$ of all validators.
[^12]: https://beaconcha.in/validators
We present a simple ex ante reorgs where an adversary, being the proposer for slot $n+1$, can perform a reorg of one block. Observe that this attack is done on the available ledger $𝖫𝖮𝖦_{\text{da}}$ (see Properties of Gasper section), and assuming synchrony.

*In slot $n + 1$ the adversary privately creates block $n + 1$ on block $n$ and attests to it. Honest validators of slot $n+1$ do not see any block and thus attest to block $n$ as head of the chain. In the next slot, an honest proposer publishes block $n + 2$ building on block $n$, which is the current head in their view. Simultaneously, the adversary finally publishes block $n + 1$ and the attestation voting for block $n + 1$. All honest validators of slot $n + 2$ attest to block $n + 1$ as head of the chain, because it has more weight than block $n + 2$. In the next slot block $n + 3$ is proposed building on block $n + 1$. Block $n + 2$ is reorged out.* [https://eprint.iacr.org/2021/1413.pdf]
*Proposer boosting does not mitigate all ex ante reorgs* [https://ethresear.ch/t/change-fork-choice-rule-to-mitigate-balancing-and-reorging-attacks/11127]. Let $W=100$ be the number of total validators per slot and let us assume that the proposal weight is $W_p = 0.8 W = 80$. Moreover, let us assume a fraction of Byzantine validators of $7\%$, i.e., we assume $7$ Byzantine validators in each slot. The attack works as it follows. The adversary proposes a hidden block for the slot $n+1$ and votes for it with $7\%$ of adversarial attestations from that slot. Thus, an honest proposer for slot $n+2$ builds its block on block $n$ (observe that block $n+2$ is now sibling of the hidden block $n+1$). Due to proposer boosting, the $93$ honest validators for slot $n+2$ vote for block $n+2$. However, the adversary again uses its $7\%$ attestations from slot $n+2$ to vote for the hidden block $n+1$.
Now, let us assume that block $n+3$ is also adversarial, and builds on $n+1$. Now the chain of block $n+1$ has $7\%$ attestations from slot $n+1$, $7\%$ attestations from slot $n+2$, and $80\%$ attestations from slot $n+3$ (due to the proposer boosting). This equals $94\%$, which is more than the $93\%$ from the honest committee of slot $n+2$. As a result, honest validators switch over and vote for block $n+3$, and block $n+2$ is forked out.
#### View-Merge As A Replacement For Proposer Weight Boosting
The notion of *view-merge*, initially introduced by the [Highway protocol](https://blog.casperlabs.io/the-casper-network-highway-consensus-protocol/), aims to solve some problems that arise with the proposer boosting technique. For example, proposer boosting can be weaponized by Byzantine proposers to conclude a reorg, lowering the amount of attestations needed for it by the weight of boost. [https://ethresear.ch/t/change-fork-choice-rule-to-mitigate-balancing-and-reorging-attacks/11127]
The idea behind the view-merge is to join the view of the honest proposer with those of all the other honest validators before they cast a vote in their slot. The result is that *in slots with a honest proposer all honest validators vote in favor of the honest proposal.* [https://arxiv.org/pdf/2209.03255.pdf]
The general concept of view-merge is the [following](https://ethresear.ch/t/view-merge-as-a-replacement-for-proposer-boost/13739):
* Attesters freeze their view $\Delta$ seconds before the beginning of a new slot, caching new messages for later processing[^8].
* The proposer, instead, does not freeze its view, and proposes, based on its view, on top of the head of the chain at the beginning of its slot. Moreover, the proposer references all attestations and blocks it used in its fork-choice in some point-to-point message, which is propagated with the block.
* Attesters include the referenced attestations in their view, and attest based on the *merged view*.
[^8]: Note that, currently, the duration of a slot in Gasper is $3\Delta$, with $\Delta$ be the message delay. In particular, the slot is divided into $3$ parts of $4$ seconds each: $4$ seconds to propose a block, $4$ seconds to attest, and $4$ seconds to aggregate the attestations (see the Implementation section).
If the network delay is less that $\Delta$, then every honest validator receives all the same messages. This implies that the view of the proposer is a superset of the frozen views of other validators. So, the final merged view is equal to the view of the proposer. Moreover, if the output of the fork-choice is a function of a view, then every honest validator has the same fork-choice output. As a consequence, honest validators attest to honest proposals.
##### Goldfish
In this section we present [Goldfish](https://arxiv.org/pdf/2209.03255.pdf), a simplified variant of LMD-GHOST, introduced by D'Amato *et al.*, that implements the notions of view-merge and equivocation discounting. Goldfish can tolerate dynamic participation, it supports subsampling of validators (at each slot, the protocol can pseudo-randomly select a small group of validators to run the protocol on behalf of the total validator set), and it is provably secure and reorg resilient in synchronous networks with dynamic participation, assuming a majority of the validators follows the protocol honestly. Finally, Goldfish implements the notion of *vote expiry*, i.e., during each slot only votes from the immediately preceding slot influence the protocol’s behavior.
The adversary decides for each round and each honest validator whether it is asleep or not. Asleep validators do not execute the protocol. Messages delivered to an asleep validator get delivered to it only once the validator is no longer asleep. When a validator stops being asleep, it becomes *dreamy*. During this phase, it joins the protocol, usually over multiple rounds, using a special *joining procedure* specified by the protocol. Upon completion of this procedure, the honest validator becomes *awake* and then follows the the protocol. Adversarial validators are always awake.
Goldfish implements a variant of GHOST, for the fork-choice rule, called **GHOST-Eph**. GHOST-Eph is a function that *takes a view $G$ and slot $t$ as input, and finds the canonical GHOST-Eph chain determined by the votes within $G$ that were cast for slot $t$. More specifically, starting at the genesis block, the function iterates over a sequence of blocks from $G$, selecting as the next block, the child of the current block with the maximum number of validators that have cast a slot $t$ vote for a block within its subtree. This continues until it reaches a leaf of the block-tree, and outputs a complete chain from leaf to root. The fork-choice rule ignores votes from before slot $t$ in its decision (votes are ephemeral), lending GHOST-Eph its name.* [https://arxiv.org/pdf/2209.03255.pdf]

*Slots in Goldfish have a duration of $3\Delta$ rounds. At the beginning of slot $t$, i.e., at round $3\Delta t$, each awake honest validator $v_i$ checks if it is eligible to propose a block for slot $t$, i.e., if $v_i$ is a leader for slot $t$, by evaluating the verifiable random function (VRF) with secret key $\mathscr{vsk}$. If $v_i$ is the leader for slot $t$, then $v_i$ identifies the tip of its canonical GHOST-Eph chain using the slot $t-1$ votes in its view, and it broadcasts a proposal message containing (i) a new block extending the tip and (ii) the union of its view and buffer, $G \cup \mathcal{B}$.* (Observe that the buffer $\mathcal{B}$ is distinct from the validator’s view $G$, the evergrowing set of messages used to make consensus decisions. Buffered messages are admitted to the view (merged) only at specific points in time.) *At round $3\Delta t + \Delta$, among the proposal messages received for slot $t$, each honest awake validator selects the one with the minimum VRF output, and accepts the block contained in the message as the proposal block for slot $t$. Moreover, validator $v_j$ merges its view with that of the proposal message. Then, with its VRF secret key $\mathscr{vsk}$, $v_j$ checks if it is eligible to vote for a block at slot $t$. If that is the case, $v_j$ identifies the new tip of its canonical GHOST-Eph chain using the slot $t − 1$ votes in its updated view, and broadcasts a slot $t$ vote for this tip.*
*At round $3\Delta t + 2\Delta$, each honest awake validator $v_j$ merges its buffer $\mathcal{B}$ containing the votes received over the period $(3\Delta t + \Delta, 3\Delta t + 2\Delta]$ with its view $G$. Then, $v_j$ identifies the new tip of its canonical GHOST-Eph chain using the slot $t$ votes in its updated view, takes the prefix of this chain corresponding to blocks from slots $\le t-\kappa$, and outputs this confirmed prefix as the Goldfish ledger.*
*At the start of the next slot, i.e., at round $3\Delta t + 3\Delta$, the buffer of any honest validator contains all the votes received by honest validators in the period $(3\Delta t + \Delta, 3\Delta t + 2\Delta]$, i.e., all the votes which they have merged into their view at round $3\Delta t + 2\Delta$. In particular, the proposal message of an honest leader includes all such votes, ensuring that the view in an honest leader’s proposal message is a superset of any honest validator’s views at round $3\Delta(t+1)+\Delta$.* [https://arxiv.org/pdf/2209.03255.pdf]

A fast confirmation rule can also be added to Goldfish, allowing validators to confirm honest blocks proposed at the tip of their canonical GHOST-Eph chains within the same slot under optimistic conditions, i.e., under high participation and honest supermajority. This is done by adding $\Delta$ more rounds to slots, which are now divided into $4\Delta$ rounds.

*At the start of each slot, the proposer merges buffered votes into their local view, determines their canonical chain, and proposes and broadcasts a block extending it, together with their local view. One-fourth into each slot, each voter merges the proposed view into their local view, determines their canonical chain, and casts a vote on the tip. Two-fourths into the slot, all awake validators merge their buffers into their local view and run the optimistic fast confirmation rule.
In particular, at round $4\Delta t + 2\Delta$, a validator merges its buffer and view, then marks a block $B$ proposed at the same slot $t$ as fast confirmed if $G$
contains a subset $G'$ of slot $t$ votes by distinct validators for $B$ such that more than $\frac{3}{4}$ of the eligible voters of slot $t$ voted for $B$. In this case, $B$ and its prefix are output as the Goldfish ledger at round $4\Delta t + 3\Delta$. If no block is fast confirmed $2\Delta$ rounds into a slot in the view of a validator, the validator uses the $\kappa$-slots-deep confirmation rule, i.e., the slow confirmation rule, at round $4\Delta t + 3\Delta$ to output the Goldfish ledger. However, validators do not roll back their ledgers: if the validator has previously fast confirmed a block within the last $\kappa$ slots, it continues to output that block.
Finally, three-fourths into the slot, all awake validators again merge their buffers into their local view, and output a ledger according to GHOST-Eph.* [https://arxiv.org/pdf/2209.03255.pdf]
Goldfish guarantees the following properties, and the proof can be found in the [full paper](https://arxiv.org/pdf/2209.03255.pdf).
* **Reorg resilience**: Suppose the validator that has the proposal with the minimum VRF output within a slot is an honest validator. Then, the block proposed by that validator enters and stays in the canonical GHOST-Eph chain adopted by any honest validator at all future slots.
* **Dynamic availability**: Under a synchronous network in the sleepy model (i.e., for GST $= 0$), the ledger output by Goldfish provides $\frac{1}{2}$-safety and $\frac{1}{2}$-liveness at all times with overwhelming probability.
Observe that $T_{\text{conf}}$ is a polynomial function of a security parameter $\kappa$. Moreover, a state machine replication protocol that outputs a ledger $\mathscr{ch}$ is $T_{\text{conf}}$-secure after time $T$, and has transaction confirmation time $T_{\text{conf}}$, if $\mathscr{ch}$ satisfies **Safety** : For any two rounds $t, t′ \ge T$, and any two honest validators $v_i$ and $v_j$ (possibly $i = j$) awake at rounds $t$ and $t′$ respectively, either ledger $\mathscr{ch}_i^t$ is the same as, or a prefix of $\mathscr{ch}_j^{t'}$ or vice-versa; and **Liveness**: If a transaction is received by an awake honest validator at some round $t \ge T$, then for any round $t′ \ge t + T_{\text{conf}}$ and any honest validator $v_i$ awake at round $t'$, the transaction will be included in $\mathscr{ch}_{t'}^i$. Ahe protocol satisfies $\frac{1}{2}$-safety ($\frac{1}{2}$-liveness) if it satisfies safety (liveness) if the fraction of adversarial validators is bounded above away from $\frac{1}{2}$ for all rounds.
Despite the security guarantees ensured by Goldfish, vote expiry as it is in this protocol leads to some problems. In particular, blocks in Goldfish do not accumulate safety against asynchrony as time goes on. This is because vote expiry after one slot means that *Goldfish cannot tolerate a single slot in which all honest validators are asleep or in which they cannot hear from the other honest validators due to adversarially induced network delay.* [https://arxiv.org/pdf/2209.03255.pdf]
##### RLMD-GHOST
Goldfish is not considered practically viable to replace LMD-GHOST in Ethereum, due to its brittleness to temporary asynchrony: even a single slot of asynchrony can lead to a catastrophic failure, jeopardizing the safety of any previously confirmed block.
D'Amato and Zanolini introduce [Recent Latest Message Driven GHOST](https://arxiv.org/pdf/2302.11326.pdf) (RLMD-GHOST), a protocol that generalizes both LMD-GHOST and Goldfish. As the former, RLMD-GHOST implements the latest message rule (LMD). As the latter, it implements view-merge and vote expiry. Differently from Goldfish, where only votes from the most recent slot are considered, RLMD-GHOST is parameterized by a *vote expiry period $\eta$*, i.e., only messages from the most recent $\eta$ slots are utilized. For $\eta = 1$, RLMD-GHOST reduces to Goldfish, and for $\eta = \infty$ to (a more secure variant of the original) LMD-GHOST.
D'Amato *et al.* introduce with Goldfish the notion of active validator (there, validators which have completed the joining protocol are simply called *awake*, and validators which are executing the joining protocol are called *dreamy*) and assume a modified condition, i.e,, $h_{r - 3\Delta} > f_{r}$, with $h_r$ the number of honest validators that are active at round $r$ and with $f_r$ the number of adversarial validators at round $r$. In this condition, that is tailored for their protocol, Goldfish, $h_{r-3\Delta}$ is considered instead of $h_r$ because, if $r$ is a voting round in Goldfish, validators corrupted after round $r$ can still retroactively cast votes for that round, which (votes) are relevant until $3\Delta$ rounds later. In practice, all that is required is that $h_{3\Delta (t-1) + \Delta} > f_{3\Delta t + \Delta}$ for any \emph{slot} $t$, i.e., the condition only needs to hold for *voting rounds*.
[D'Amato and Zanolini](https://arxiv.org/pdf/2302.11326.pdf) follow this distinction between awake and active validators, and use $H_t$ and $A_t$, for a slot $t$, to refer to the set of active and adversarial validators at round $3\Delta t + \Delta$, respectively. Moreover, $H_{s, t}$ denote the set of validators that are active *at some point* in slots $[s,t]$, i.e., $H_{s,t} = \bigcup_{i=s}^t H_i$ (if $i < 0$ then $H_i = \emptyset$). Then, for some fixed parameter $1\leq \tau \leq \infty$, the following condition, which is referred to as *$\tau$-sleepiness at slot $t$*, holds for any slot $t$ after GST:
$$|H_{t-1}| > |A_{t} \cup (H_{t-\tau, t-2}\setminus H_{t-1})|.$$
The sleepy model in which the adversary is constrained by $\tau$-sleepiness after GST is called the *$\tau$-sleepy model*. Note that, for $\tau = 1$, this reduces to the sleepy model from Goldfish, as this condition reduces to the majority condition $h_{r - 3\Delta} > f_{r}$ of Goldfish for voting rounds $r = 3\Delta t + \Delta$, because $H_{t-1, t-2} = \emptyset$.
RLMD-GHOST is implemented in the *$\tau$-sleepy model*, which allows for more generalized and stronger constraints in the corruption and sleepiness power of the adversary. In other words, the honest validators that are actively participating in the consensus protocol at slot $t$ are always more than the adversarial validators together with the honest validators that actively participated in the protocol during *some* slots before $t$ and that now, at slot $t$, are not anymore participating (i.e., we count them as adversarial). For instance, in LDM-GHOST, *some slots before $t$* translates into *every slot starting from the genesis*, while for Goldfish this transaltes into *one slot before $t$*.
RLMD-GHOST proceeds in *slots* consisting of $3\Delta$ rounds, each having a proposer $v_p$, chosen through a proposer selection mechanism among the set of validators. In particular, at the beginning of each slot $t$, the proposer $v_p$ proposes a block $B$. Then, all active validators vote after $\Delta$ rounds for block, after having merged their *view* with the view of the proposer. Moreover, every validator $v_i$ has a buffer $\mathcal{B}_i$, a collection of messages received from other validators, and a view $G_i$, used to make consensus decisions, which admits messages from the buffer only at specific points in time, i.e., during the last $\Delta$ rounds for a slot. The need for a buffer is to prevent [some attacks](https://ethresear.ch/t/view-merge-as-a-replacement-for-proposer-boost/13739). RLMD-GHOST is characterized through a deterministic fork-choice rule **RLMD-GHOST**, which is used by honest proposers and voters to decide how to propose and vote, respectively, based on their view at the round in which they are performing those actions. In particular, the fork-choice rule that D'Amato and Zanolini implement considers the last (non equivocating) messages sent by validators that are not older than $t − \eta$ slots, in order to make protocol’s decisions.

RLMD-GHOST results in a synchronous protocol that has interesting practical properties: it is dynamically available and reorg resilient in the *$\tau$-sleepy model*, assuming that the honest validators that are actively participating in the consensus protocol at slot $t$ are always more than the adversarial validators (that actively participate in the protocol) together with the validators that actively participated in the protocol during $\eta$ slots before $t$ and that now, at slot $t$, are not anymore participating (i.e., we count them as adversarial). Moreover, RLMD-GHOST is resilient to asynchronous periods lasting less than $\eta-1$ slots.
As one can observe, both RLMD-GHOST and Goldfish (and also LMD-GHOST) have the same structure: first there is a proposing phase, then a voting phase, and finally a merge phase. [D'Amato and Zanolini](https://arxiv.org/pdf/2302.11326.pdf) generalize this structure by defining *propose-vote-merge* protocols. These are protocols that proceed in *slots* consisting of *k* rounds, each having a proposer $v_p$, chosen through a proposer selection mechanism among the set of validators. In particular, at the beginning of each slot $t$, the proposer $v_p$ proposes a block $B$. Then, all active validators vote after $\Delta$ rounds. The last $\Delta$ rounds of the slot are needed for the *view-merge* synchronization technique. Propose-vote-merge protocols are defined through a deterministic fork-choice rule $FC$, which is used by honest proposers and voters to decide how to propose and vote, respectively, based on their view at the round in which they are performing those actions (in the case of Goldfish, the fork-choice rule is **GHOST-Eph**, while in the case of RLMD-GHOST the fork-choice rule is **RLMD-GHOST**). A propose-vote-merge protocol proceeds in three phases:
**Propose**: In this phase, which starts at the beginning of a slot, the proposer $v_p$ merges its view $G_p$ with its buffer $\mathcal{B}_p$, i.e., $G_p \gets G_p \cup \mathcal{B}_p$, and sets $\mathcal{B}_p \gets \emptyset$. Then, $v_p$ runs the fork-choice rule $FC$ with inputs its view $G_p$ and slot $t$, obtaining the head of the chain $B' = FC(G_p, t)$. Proposer $v_p$ extends $B'$ with a new block $B$, and updates its canonical chain accordingly. Finally, it broadcasts the proposal message to every validator.
**Vote**: Here, every validator $v_i$ that receives a proposal message from $v_p$ merges its view with the proposed view $G$, by setting $G_i \gets G_i \cup G$. Then, it broadcasts votes for some blocks based on its view.
**Merge**: In this phase, every validator $v_i$ merges its view with its buffer, i.e., $G_i \gets G_i \cup \mathcal{B}_i$, and sets $\mathcal{B}_i \gets \emptyset$.
#### Path towards single slot finality
Currently, Gasper takes between 64 and 95 slots to finalize blocks. Because of that, a significant portion of the chain is susceptible to reorgs. The possibility to capture MEV (Maximum Extractable Value) through such reorgs can then disincentivize honestly following the protocol, breaking the desired correspondence of honest and rational behavior. Moreover, the relatively long time to finality forces users to choose between economic security and faster transaction confirmation. This motivates the study of the so-called [single slot finality](https://notes.ethereum.org/@vbuterin/single_slot_finality) protocols: consensus protocols that finalize a block in each slot and, more importantly, that finalize the block proposed at a given slot within such slot. A relevant video about single slot finality by Vitalik Buterin can be found [here](https://www.youtube.com/watch?v=nPgUKNPWXNI).
[D'Amato and Zanolini](https://arxiv.org/pdf/2302.12745.pdf) propose a protocol that combines [RLMD-GHOST](https://arxiv.org/pdf/2302.11326.pdf) with a finality gadget, resulting in a secure ebb-and-flow protocol that can finalize one block per slot. Importantly, the protocol they present can finalize the block proposed in a slot, within such slot.
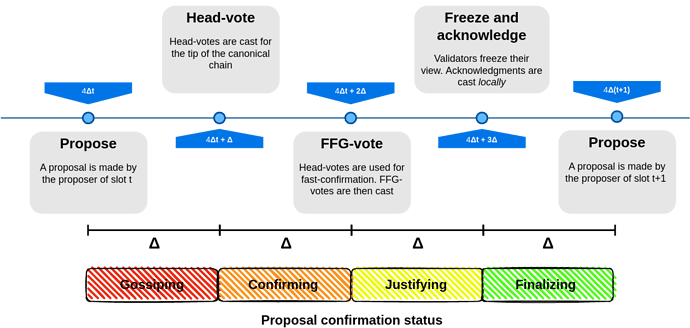
Differently from the version of RLMD-GHOST presented above, here RLMD-GHOST proceeds in slots consisting of $4\Delta$ rounds with *fast confirmation*, as summarized in the following figure.
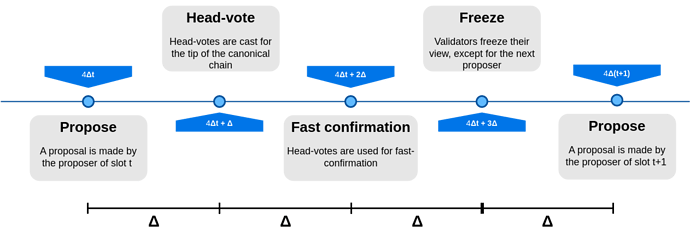
In the figure above, head-votes represent votes cast with respect to RLMD-GHOST protocol, i.e., the dynamically available protocol/component. To be more specific, a head vote is a tuple [HEAD-VOTE, $B$, $t$, $v$], where $B$ is a block, $t$ is the slot in which the vote is cast, and $v$ is the validator that cast the vote. The single slot finality protocol presented by D'Amato and Zanolini introduces a new type of vote, i.e., the FFG vote. In particular, FFG vote is a tuple [FFG-VOTE, $\mathcal{C}_1$, $\mathcal{C}_2$, $v$], where $\mathcal{C}_1, \mathcal{C}_2$ are checkpoints, with $\mathcal{C}_1.t < \mathcal{C}_2.t$, and $\mathcal{C}_1.B$ is a prefix of $\mathcal{C}_2.B$. [^9] These two checkpoints are referred to as *source* and *target*, respectively, following the notation of Gasper, and to FFG votes as *links* between source and target. The FFG component of the SSF protocol presented by D'Amato and Zanolini takes inspiration from Casper and aims at finalizing one block per slot by counting ffg votes cast at a given slot.
[^9]: A checkpoint is justified in a view $G$ if $G$ contains the chain of supermajority links justifying it. The justified checkpoint $\mathcal{C}$ of highest slot $\mathcal{C}.t$ in $G$ is referred, as in Gasper, as the *latest justified checkpoint* in $G$, or $\mathcal{LJ}(G)$, and to $\mathcal{LJ}(G).B$ as the *latest justified block* in $G$, or $LJ(G)$. Ties are broken arbitrarily, and the occurrence of a tie implies that $\frac{n}{3}$ validators are slashable for equivocation. For brevity, $\mathcal{LJ}_i$ refers to $\mathcal{LJ}(G)$, the latest justified checkpoint in the view $G_i$ of validator $v_i$. A checkpoint $\mathcal{C}$ is *finalized* if it is justified and there exists a supermajority link $\mathcal{C} \to \mathcal{C}'$ with $\mathcal{C}'.t = \mathcal{C}.t + 1$. A block $B$ is finalized if there exists a finalized checkpoint $\mathcal{C}$ with $B = \mathcal{C}.B$.
In the protocol by D'Amato and Zanolini, head votes work exactly as in RLMD-GHOST, or any propose-vote-merge protocol, i.e., validators vote for the output of their fork-choice rule: when it is time to vote, validator $v_i$ casts vote [HEAD-VOTE, $FC(G_i, t), t, v_i$]. Here, the fork-choice rule adopted is the same as **RLMD-GHOST**, with the only difference that the view $G_i$ has filtered out branches which do not contain $LJ(G)$, the latest justified block.
FFG votes always use the latest justified checkpoint as source. The target block is the highest confirmed descendant of the latest justified block, or the latest justified block itself if there is none. The target checkpoint is then $\mathcal{C}_{\text{target}} = (\text{argmax}_{B \in \{LJ_i, \mathsf{chAva}\}}|B|,t)$, and the FFG vote of $v_i$ is [FFG-VOTE, $\mathcal{LJ}_i, \mathcal{C}_{\text{target}}, v_i$], voting for the link $\mathcal{LJ}_i \to \mathcal{C}_{\text{target}}$. Here, $\mathsf{chAva}$ is the dynamic available chain output by the RLMD-GHOST protocol.
Finally, a slot in the SSF protocol follows this structure
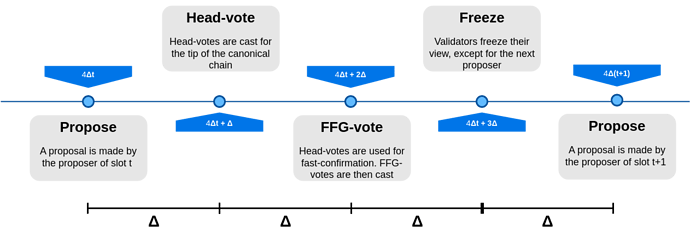
When a proposer is honest, the network is synchronous, and an honest supermajority is online, the outcome is that the proposal gets fast confirmed and then justified, before the end of the slot. Moreover, if honest validators see the justification before the next slot, they will never cast an FFG vote with an earlier source, and so the proposal will never be reorged, even if later the network becomes asynchronous.
The SSF protocol is implemented by the following algorithm

##### Acknowledgments
In this protocol, *blocks proposed by honest proposers under good conditions have very strong reorg resilience guarantees. On the other hand, their unreorgability is not known to observers by the end of the slot, and moreover no economic penalty can yet be ensured in case of a reorg, so we rely at this point on honesty assumptions. Finality is only achieved at the earliest after two slots. In order to truly have single slot finality, in the sense that an honest proposal can be finalized (and is finalized, under synchrony) within its proposal slot, then another FFG voting round can be added, or, as D'Amato and Zanolini decided to do in the paper, validators send a different type of message acknowledging the justification. For example, if the checkpoint $(B,t)$ is justified at slot $t$, validators can send the acknowledgment message $((B,t), t)$, confirming their knowledge of the justification of $(B,t)$. This way, they signal that in future slots they will never cast an FFG vote with a source from a slot earlier than $t$. A slashing condition can be attached to this, almost identical to surround voting: it is slashable to cast an acknowledgment $((C,t),t)$ and an FFG vote $(A,t') \to (B,t'')$ with $t' < t < t''$, i.e., where the FFG vote surrounds the acknowledged checkpoint. Then, if 2/3 of the validators cast an acknowledgment, one can finalize the acknowledged checkpoint.* [https://ethresear.ch/t/a-simple-single-slot-finality-protocol/14920]
The complete protocol is then the following