# EVM384 Update 5: First Gas Cost Estimates
Text jointly authored by (in alphabetic order by last name) Alex Beregszaszi, Pawel Bylica, Casey Detrio, Paul Dworzanski, and Jared Wasinger with help from the entire Ewasm team.
[TOC]
## Introduction
This is a continuation of a series of updates on EVM384.
[Preview of EVM384](https://notes.ethereum.org/@axic/evm384-preview)
[Update 1: Can we do fast crypto in EVM?](https://notes.ethereum.org/@axic/evm384)
[Update 2: The Interfaces](https://notes.ethereum.org/@poemm/evm384-interface-update)
[Update 3: The Miller Loop](https://notes.ethereum.org/@poemm/evm384-update3)
[Update 4: The Final Exponentiation](https://notes.ethereum.org/@poemm/evm384-update4)
Feedback and discussions occur on allcoredevs chat, allcoredevs calls, and on [this magicians thread](https://ethereum-magicians.org/t/evm384-feedback-and-discussion/4533).
In this update, we propose initial gas costs for EVM384. But first we explain the gas cost situation in EVM.
## Background on EVM Gas Costs
Gas simultaneously limits runtime, state access, and state growth, among other things. For now, the simplicity of a single metric of gas outweighs the inefficiencies inherent from its oversimplicity. With this single metric, it would at least be nice if gas costs were somewhat consistent across operations.
In 2015, original gas costs were assigned with benchmarks and formulas in [this original document](https://docs.google.com/spreadsheets/d/1m89CVujrQe5LAFJ8-YAUCcNK950dUzMQPMJBxRtGCqs/edit). Since these original assignments, we have sped up EVM implementations, in particular, [evmone](https://github.com/ethereum/evmone). Geth's EVM also has a list of speedups, including the [uint256](https://github.com/holiman/uint256) library, with more to speedup opportunities identified. Because of these implementation speedups, and the speedups from newer hardware, gas costs have deviated from the original benchmarks. These speedups have not been reflected in gas costs. So gas mispricing has become a topic of discussion.
Gas costs have been exploited in DoS attacks, the most famous were the Shanghai attacks. Often, gas cost attacks involve second-order interactions between the system state and different opcodes. For example, the Shanghai attacks targeted client-specific caching, and were amplified by recursive calls. Because of these DoS attacks, there have been gas price security fixes, included [EIP-150](https://eips.ethereum.org/EIPS/eip-150) in Tangerine Whistle, [EIP-1884](https://eips.ethereum.org/EIPS/eip-1884) in Istanbul, and [EIP-2929](https://eips.ethereum.org/EIPS/eip-2929) due with Berlin. Even after years of hardening, critical gas pricing anomalies are still [reported](https://arxiv.org/abs/1909.07220) and fixed. Nevertheless, gas cost attacks remain one of the biggest threats to Ethereum security.
Metering is difficult. Hardware is designed to "do the common case fast", but allows bottlenecks for uncommon cases. These hardware bottlenecks can be exploited by an attacker. And proprietary hardware makes it impossible for us to decide what the worst-case bottlenecks are. So metering must necessarily be conservative enough to tolerate hardware bottlenecks.
Because of these security risks, core developers have become averse to changes, and strongly prefer simple opcodes with constant gas costs to minimize consensus code -- i.e. the trusted compute base.
In our opinion, the metering problem, i.e. precisely estimating runtime of user-deployed code across a distributed consensus system, is an open problem. And until this problem is solved, there is a metering inefficiency which creates a gap between EVM bytecode and hand-tuned native code.
With EVM384, the strategy is to shrink this performance gap by focusing on covering bottlenecks of a wide class of crypto algorithm with a few additional basic EVM opcodes.
These new opcodes retain the inherent limitations of the EVM. Below, we address these limitations. But first we propose gas costs and present concrete examples to illustrate these limitations.
## Proposed EVM384 Gas Costs
We have reviewed multiple models to determine the pricing of EVM384 instructions. See [Appendix A](#Appendix-A-Model-A-%E2%80%94-The-BaseOperation-Gas-Model) for an explanation of Model A, and [Appendix B](#Appendix-B-Model-B-%E2%80%94-Costs-Relative-to-Keccak256) for an explanation of Model B.
---
| | Model A | Model B |
| --- | --- | --- |
|`ADDMOD384` | 2 gas | 1 gas |
|`SUBMOD384` | 2 gas | 1 gas |
|`MULMODMONT384`| 6 gas | 3 gas |
**Table 1.** Proposed gas costs for each model.
---
For the remainder of this document, we apply these gas costs to cryptographic operations, and discuss how to overcome various bottlenecks. But first we count opcodes for some cryptographic operations.
## Opcode Counts of Cryptographic Operations
[Our implementation](https://github.com/poemm/EVMcurves) has focused on the two biggest building blocks of the pairing equation check: the miller loop and final exponentiation for BLS12-381. Although we did implement many subroutines which can be reused to implement other operations.
In Table 2 we provide detailed counts of each opcode used by our implementations.
**Note: these implementations are baseline prototypes for simplicity. Some optimizations are omitted.**
---
| | Miller Loop | Final Exponentiation |
| --- | --- | --- |
| ADDMOD384 | 12182 | 24370
| SUBMOD384 | 11786 | 13867
| MULMODMONT384 | 6867 | 8196
| PUSH16 | 30835 | 45988
| PUSH2 | 3181 | 7546
| PUSH1 | 265 | 839
| PUSH8 | 62 | 0
| PUSH32 | 4 | 21
| MSTORE | 1536 | 3649
| MLOAD | 1532 | 3610
| JUMPDEST | 129 | 421
| JUMPI | 124 | 315
| JUMP | 0 | 141
| DUP* | 124 | 796
| SUB | 62 | 315
| SHR | 62 | 0
| XOR | 62 | 0
| SWAP1 | 62 | 315
| AND | 62 | 0
| CALLDATACOPY | 1 | 1
| RETURN | 1 | 1
| POP | 1 | 35
**Table 2.** Opcode counts for miller loop and final exponentiation.
---
Observe the following:
- `PUSH16` is used heavily to provide the operand memory offsets to EVM384 instructions. (Though we sometimes use `DUP` to prepare the memory offsets for EVM384 opcodes, so the count of `PUSH16` does not match the counts of `ADDMOD384`, `SUBMOD384`, and`MULMODMONT384`.)
- Other `PUSH` opcodes are also non-negligble. Similarly for `DUP` opcodes.
- `MLOAD` and `MSTORE` are also non-negligible. They are mostly used in memory copies, a common operation which we will address below.
To estimate costs of cryptosystems which use pairing equation checks, we can use our implementations above. A n-pairing equation check can be done with n miller loops and one final exponentiation, plus n-1 f12muls which have 115 `ADDMOD384`, 109 `SUBMOD384`, and 54 `MULMODMONT384` each, plus some negligible other costs. It is safe to say this additional work is less than 1% of the cost of miller loops and final exponentiation. Also notable is that pairings also use subgroup checks, which are known to add ~15% overhead, but we omit subgroup checks because they can sometimes be skipped. On the other hand, implementation optimizations are also omitted, some of which we discuss below.
These opcode counts give context for the rest of this document.
## Removing Bottlenecks
### Cost of PUSH: Interface v9
Our current prototyping EVM384 interface is [v7](https://notes.ethereum.org/@poemm/evm384-interface-update#Interface-v7), where each EVM384 instruction pops a stack item of packed memory offsets. v7 is preferred because it is generic enough to allow programatically manipulating input offsets and is similar in design to other opcodes. The downside of v7 is that we must put something on the stack before each EVM384 opcode -- our prototypes mostly use `PUSH16`. But each `PUSH16` costs three gas, which is significant. Even if the gas cost of `PUSH16` is reduced, there is still stack overhead.
To prepare for the possibility that v7 stack overhead is too significant, we consider another interface, [v9](https://notes.ethereum.org/@poemm/evm384-specs#Interface-Version-9), to remove stack overhead altogether. We do this by encoding the offsets for each EVM384 opcode directly after the opcode as an immediate. The downside of v9 is that we may need EVM versioning because immediates can [break old bytecode](https://ethereum-magicians.org/t/eip-663-unlimited-swap-and-dup-instructions/3346/10).
Corresponding v7 and v9 bytecode use the same number of EVM384 opcodes, but v9 uses significantly fewer non-EVM384 opcodes, since it skips the `PUSH16`. This results in a significant cost reduction.
Note that our v9 measurements below come from manually subtracting `PUSH16` costs from v7 measurements, everything else is identical.
### Cost of PUSH and DUP: Repricing
As emphasized previously, EVM384v7 opcodes are preceded by `PUSH16`, which currently costs three gas. We are considering proposing a gas cost reduction of `PUSH*` to two gas. This is justified because `PUSH*` is similar to opcodes like `ADDRESS` and `CALLER` which cost two gas. We are considering a similar reduction for `DUP*`. Note that we have not considered a similar reduction for `SWAP*`, given that it reorders the stack and is sufficiently different to `PUSH*` and `DUP*`.
### Memory Manipulation Cost
After EVM384 opcodes and `PUSH`, the cost of `MLOAD` and `MSTORE` is the next biggest bottleneck. These are mostly used for memory copy operations, which we perform with `PUSH<from_offset> MLOAD PUSH<to_offset> MSTORE` for each 32 byte word. We are considering three options to reduce this bottleneck: (i) reducing the price of these opcodes, (ii) using `ADDMOD384` for copies, or (iii) a new bulk `MCOPY` opcode. Our gas costs below are conservative and don't include options (ii) or (iii).
### INVERSEMOD384 and SQUAREROOTMOD384
Non-primitive operations such as modular inverse and square root are often used in cryptography. One option is to use the `modexp` precompile to do these operations, but we found that even with the `modexp` repricing ([EIP-2565](https://eips.ethereum.org/EIPS/eip-2565)) it is less expensive to do it in pure EVM384 with addition chains. But we note that these operations are recurring, so we are open to new opcodes for these operations, which would reduce gas costs further.
### Implementation Optimizations
Our implementations are baselines, omitting optimizations for simplicity. But we have identified many optimization opportunities. For example, some of our bit iterator loops are generic with extra overhead each iteration.
There are also optimizations in the cryptography implementation. For example, the subroutine `f2mul` can be implemented in several ways, with `f2mul_v3` being common in native implementations, and our `f2mul_v4` having one more `MULMODMONT384` and three fewer `ADDMOD384` and `SUBMOD384`. This tradeoff saves gas under many gas cost options. Next we give opcode counts for our operations with different `f2mul` implementations. Bytecode for `f2mul_v3` is [here](https://github.com/poemm/EVMcurves/tree/evm384-update5), and for `f2mul_v4` edit the function `gen_f2mul()` in `genhuff.py` substituting `case=3` with `case=4`. Please note that `f2mul_v4` is not recommended for use at the moment.
---
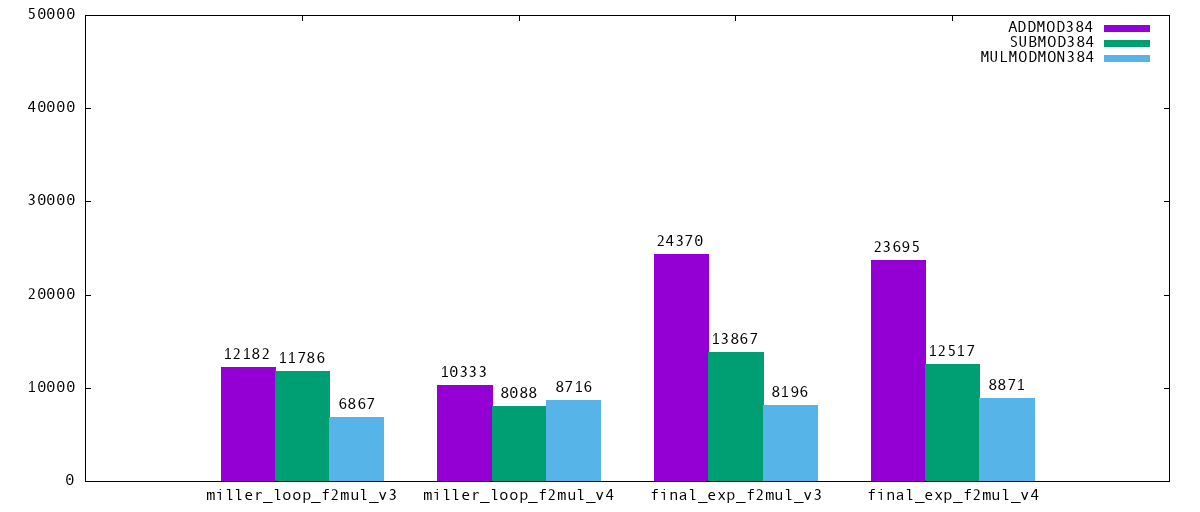
**Figure 1.** Opcode count differences of EVM384 instructions between the f2mul v3 and v4 versions.
---
Observe that these versions have non-negligible changes in overall operation counts, which can make a big difference in overall gas costs. These two `f2mul` versions highlight how optimizing for EVM is different than optimizing for native, since the EVM overhead adds cost to each operation.
Perhaps the biggest optimizations are use-case-specific optimizations, for example precomputing parts of the miller loop if one of the inputs is fixed. An open research direction is developing algorithms and tuning implementations for on-chain EVM, which has different constraints than native implementations.
### EVM Repricing
Above in the [background on EVM gas costs](#Background-on-EVM-Gas-Costs), we mention that pricing of EVM instructions has been mostly set five years ago, and did not receive a comprehensive review since. Original gas prices may have deviated from actual runtimes.
There is ongoing work investigating actual runtime costs of instructions in a [naive EVM implementation](https://github.com/ethereum/evmone#baseline-interpreter) based on a [set of synthetic benchmarks](https://github.com/ethereum/evmone/pull/278). These benchmarks aim to show a safe lower bound on costs for various instructions. A report of this effort will be released separately. In the following estimates we consider the cost of `JUMPDEST`, `PUSH*`, `DUP*`, `MSTORE`, and `MLOAD` based on these initial results.
Another issue for EVM is that gas currently has a low resolution. Most opcodes cost three gas. With the exception of state accessing opcodes and some heavy computation and control flow, almost all opcodes cost less than six gas. Opcodes with much different runtimes get rounded up to the same gas cost (for example proposed EVM384 gas costs are rounded up from 1.1 to 2 gas) because the gas resolution is too low to precisely render their gas costs. Therefore we consider [particle gas costs](https://eips.ethereum.org/EIPS/eip-2045) to improve the resolution of metering. These more granular numbers are the results of the same synthetic benchmarks.
## Gas Estimates for BLS12-381 Operations
<small>All the sources for the figures can be [found here](https://github.com/ewasm/evm384_f6m_mul/tree/update5/update5).</small>
Now we consider gas costs based on the experiments and future work above. The following tables show various gas cost options, including options which apply various optimisations.
---
| | Model A | +PUSHDUP2†† | +EVM repricing | +EVM repricing (with fractional gas) |
|---------------|---------|-----------|----------------|--------------------------------------|
| ADDMOD384 | 2 | 2 | 2††† | 1.1††† |
| SUBMOD384 | 2 | 2 | 2††† | 1.1††† |
| MULMODMONT384 | 6 | 6 | 5††† | 5.0††† |
| PUSH* | 3† | 2 | 1 | 0.9 |
| DUP* | 3† | 2 | 1 | 0.7 |
| MSTORE | 3† | 3 | 1 | 0.8 |
| MLOAD | 3† | 3 | 1 | 1.0 |
† Unchanged from current Istanbul pricing.
†† Repricing PUSH* and DUP* only.
††† Using model A with base cost 0.4 gas.
**Table 3.** Various options for pricing based on Model A.
---
| | Model B | +PUSHDUP2†† | +EVM repricing | +EVM repricing (with fractional gas) |
|---------------|---------|-----------|----------------|--------------------------------------|
| ADDMOD384 | 1 | 1 | 1 | 0.8 |
| SUBMOD384 | 1 | 1 | 1 | 0.7 |
| MULMODMONT384 | 3 | 3 | 3 | 3.0 |
| PUSH* | 3† | 2 | 1 | 0.9 |
| DUP* | 3† | 2 | 1 | 0.7 |
| MSTORE | 3† | 3 | 1 | 0.8 |
| MLOAD | 3† | 3 | 1 | 1.0 |
† Unchanged from current Istanbul pricing.
†† Repricing PUSH* and DUP* only.
**Table 4.** Various options for pricing based on Model B.
---
We highlight that some gas cost options will be non-intrusive with current EVM, other options will require minor repricings or changes, but many options will require major repricings and changes. We use the following labels, which we compose to describe options in the figures below:
- `modela` and `modelb` are based on the proposed EVM384 gas cost models above without other modifications, and give baselines to apply optimizations.
- `pushdup2` is for the PUSHDUP2 option, which reprices `PUSH*` and `DUP*` to two gas each.
- `repriced` is for the EVM repricing option, which will require security analysis from EVM experts covering important client implementations and addressing interactions between opcodes as well as hardware bottlenecks.
- `fractional` is for the `repriced` option but without rounding. Fractional gas will require a stronger security analysis, as well as updating clients to maintain fractional gas available and consensus on how to handle fractional gas at execution boundaries.
- `v7` and `v9` are for the EVM384 interface versions. In particular, `v9` omits the need for a `PUSH16`, but requires addressing possible bytecode breaking.
Next we present gas costs for miller loop and final exponentiation under various gas cost options.
---
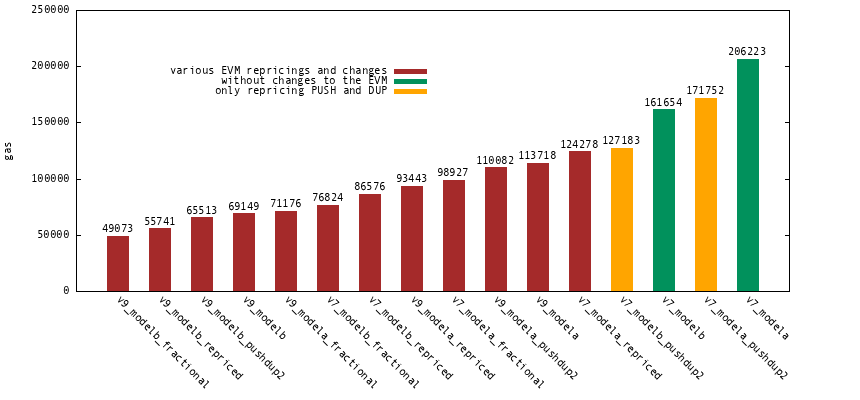
**Figure 2.** Potential gas cost estimates for a BLS12-381 miller loop in EVM384.
---
---
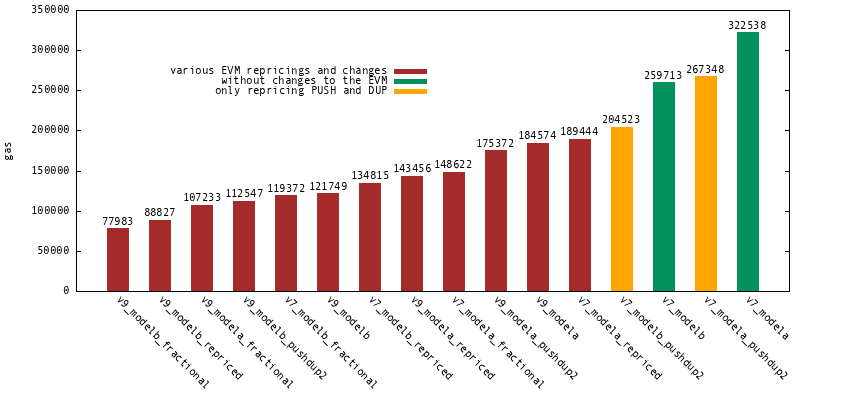
**Figure 3.** Potential gas cost estimates for a BLS12-381 final exponentiation in EVM384.
---
*Recall that a n-pairing equation check is dominated by n miller loops and one final exponentiation.*
From Figure 2 and Figure 3 we observe the following.
- Interface v9 gives significant cost improvements, but the improvements are less significant as we make other improvements.
- While opting for interface v7, a conservative repricing of `PUSH` and `DUP` to two gas would provide significant cost reductions.
- Further investigation into repricing EVM instructions would be very beneficial for computation heavy use cases.
So what is a good gas cost option? Consider `v7_modelb_repriced`. This option requires no bytecode versioning changes and no changes to consensus involving fractions of gas. It only requires an EVM repricing. Such a repricing would have benefits for everyone and is worth pursuing anyway.
These gas cost numbers omit optimizations such as `f2mul` and `MCOPY`, which could bring another 5-10% improvement for `v7_modelb_repriced`. Not to speak of other optimizations.
## Conclusion
With these gas cost measurements, we turn our attention to writing an EIP for EVM384. We are particularly interested in feedback about applications of EVM384. Along with applications, we welcome discussion about whether the three EVM384 opcodes, `ADDMOD384`, `SUBMOD384`, and `MULMODMONT384` are "complete" in covering all bottlenecks for many useful cryptosystems. Now is a good time to suggest more primitive building blocks as opcodes. For example, we would like to know whether a fourth EVM384 opcode, `INVERSEMOD384`, would be useful. Finally, we encourage discussions of generalizations of EVM384, for example to EVM768 which has several use-cases.
Finally, we are open to feedback about security and runtime attacks against our proposed EVM384 gas costs.
## Appendix A: Model A — The Base+Operation Gas Model
First a description of our base+operation cost metering model. Without loss of generality, we target 10 million gas per 100ms, which equals 1 gas per 10ns. We consider typical client hardware (three year old mid-grade laptops and mid-grade VMs). Our pricing model assigns gas cost as the sum of two components: "base cost" and "operation cost". A base cost of 1 gas (i.e. 10ns) accounts for the EVM interpreter loop, including fetching the next opcode, updating gas available, and checking for halting conditions. This base cost is illustrated with `JUMPDEST`, a no-op which costs 1 gas. To this base cost we add an operation cost which corresponds to the runtime of the opcode's operation.
This gas model is naive because it ignores how opcodes interact with each other, and with the state of the system. So a security analysis is required to identify potential attacks. We link to such an analysis below.
Using this this gas metering model, the following table has runtimes and resulting gas costs we propose for EVM384.
---
| | base gas cost | operation runtime | operation gas cost | total gas cost (base+operation) |
| --- | --- | --- | --- | --- |
| `ADDMOD384` | 1 gas | 6.4 ns | 1 gas | 2 gas |
| `SUBMOD384` | 1 gas | 5.6 ns | 1 gas | 2 gas |
| `MULMODMONT384` | 1 gas | 43.6 ns | 5 gas | 6 gas |
**Table A1.** Runtimes and gas costs of EVM384 opcodes. Runtimes are measured in [Appendix A1](#Appendix-A1-Estimation-of-new-instructions’-runtime-cost).
---
Now we consider whether these gas costs allow DoS attacks to amplify runtime. EVM384 opcodes are unique in how they access many memory locations. In particular, we must consider big slowdowns to access distant cashes and memory. An initial security analysis of potential attacks introduced by EVM384 is discussed [here](https://notes.ethereum.org/@poemm/EVM384SecurityAnalysis). To limit the severity of some potential attacks, we are evaluating reducing each packed offset to two bytes to limit addressable memory to 64kb. We solicit further security analysis.
Now we consider whether our EVM384 costs are consistent with other EVM opcodes. `ADDMOD384` and `SUBMOD384` are most similar to `ADD` and `SUB`, which are overpriced relative to our `ADDMOD384` and `SUBMOD384` benchmarks. Note that `ADDMOD` is more expensive because it is more generic than `ADDMOD384`. `MULMODMONT384` may be most similar to `MULMOD` which costs eight gas, but `MULMOD` is more generic. So our EVM384 costs are not too inconsistent or underpriced relative to the rest of EVM, except for `MSTORE` and `MLOAD`, which we discuss in our security analysis linked in the previous paragraph.
## Appendix A1: Estimation of new instructions' _runtime_ cost
Here we give more detail about the instruction benchmarks. Four different implementations have been measured on multiple machines.
#### Implementations
1. [bigint.h](https://github.com/poemm/bigint_experiments) — simple C library for big integer and modulus arithmetic.
2. [BLST](https://github.com/supranational/blst) — x86-64 assembly implementation from the BLS12-381 signature library. This assembly code is currently being [formally verified]( https://github.com/GaloisInc/BLST-Verification).
3. [Go](https://github.com/jwasinger/go-ethereum/tree/evm384-v7) — pure Go EVM384 implementation.
4. [Go/BLST assembly](https://github.com/jwasinger/go-ethereum/tree/evm384-v7-blstasm) — the above with `MULMODMONT384` implementation replaced by x86-64 assembly provided by BLST.
The first two benchmarks are easy to reproduce using [this script](https://gist.github.com/poemm/b0642c11764e81e7eaa125f1855474e3). The Go benchmarks are done with `go test`.
#### Benchmark results
The collected benchmark results and analysis can be found in [EVM384 instruction implementation benchmarks](https://docs.google.com/spreadsheets/d/1YH7wag48DNE8ckiblpSoe5thoH3FmlmtNsSXIC_DIv0/edit?usp=sharing) spreadsheet.
At this point we have eliminated the results for pure Go `MULMODMONT384` implementation for having very slow timings compared to every other implementation. We are optimistic that this implementation can be greatly improved by porting the BLST implementation to Go's [`math/bits`](https://golang.org/pkg/math/bits/) intrinsics (as has been done for `ADDMOD384` and `SUBMOD384` already).
Our final estimates are based on the BLST assembly implementation.
| | Runtimes | Mean | Fractional operation gas | Rounded operation gas |
|---------------|-----------------------|------|--------------------------|-----------------------|
| ADDMOD384 | 8, 7, 4, 7, 6 ns | 6.4 | 0.64 | 1 |
| SUBMOD384 | 6, 6, 4, 6, 6 ns | 5.6 | 0.56 | 1 |
| MULMODMONT384 | 51, 43, 30, 44, 50 ns | 43.6 | 4.36 | 5 |
**Table A2.** Summary of runtime measurements. We take the mean of the runtimes observed across five different machines, E5-2673, i7-6500U, i7-8565U, i5-5300U, and i5-6360U, respectively.
## Appendix B: Model B — Costs Relative to Keccak256
As another supporting point of evidence that the proposed costs for EVM384 opcodes are justified, we present an EVM384 opcode cost estimate based on benchmarks of the `KECCAK256` opcode.
EVM384 opcodes and `KECCAK256` behave similarly: They load data from memory as specified by an input offset, perform a computation and store a result in memory. If the memory space is small (within the CPU cache), we can assume that the difference in overhead of loading a single value (in the case of `KECCAK256`) vs several (in the case of EVM384) is minimal.
Based on this assumption we can establish a cost for EVM384 opcodes relative to `KECCAK256` by solving for the unknown EVM384 cost:
```
keccak_op_time * num_iterations / keccak_gas_cost = keccak_gas_rate
evm384_op_time * num_iterations / evm384_op_cost = evm384_gas_rate
```
For consistency, the gas rates (right-hand-sides) must be equal, so we set the left-hand-sides equal and solve for `evm384_op_cost`.
*Note: these numbers use the `KECCAK256` gas cost of Istanbul. Comparing against [EIP-2666](https://eips.ethereum.org/EIPS/eip-2666) prices would reduce the cost further.*
Below, we present the results of [benchmarks](https://github.com/jwasinger/evm384-benchmarks/tree/keccak256-bench) which calculate EVM384 opcode costs against keccak with different input sizes. Rationale: 32 bytes is the word size of EVM, 136 bytes is the Keccak round size, and 192 bytes is the maximum amount of memory read by an EVM384 operation.
#### Geth (Go-assembly implementation of mulmodmont384)
keccak input size (bytes) | number of iterations | evm384 opcode | estimated price |
--------------------| -- | --------------------- | -------- |
32 | 5000 | addmod384 | 0.71
32 | 5000 | submod384 | 0.59
32 | 5000 | mulmodmont | 3.0
32 | 50000 | addmod384 | 0.53
32 | 50000 | submod384 | 0.59
32 | 50000 | mulmodmont | 2.4
136 | 5000 | addmod384 | 0.25
136 | 5000 | submod384 | 0.42
136 | 5000 | mulmodmont384 | 2.6
136 | 50000 | addmod384 | 0.27
136 | 50000 | submod384 | 0.41
136 | 50000 | mulmodmont384 | 1.66
192 | 5000 | addmod384 | 0.78
192 | 5000 | submod384 | 0.67
192 | 5000 | mulmodmont384 | 3.0
192 | 50000 | addmod384 | 0.80
192 | 50000 | submod384 | 0.63
192 | 50000 | mulmodmont384 | 2.5
**Table A3.** Cost estimates based on geth.
#### Evmone (x86-assembly implementation of mulmodmont384)
keccak input size (bytes) | number of iterations | evm384 opcode | estimated price |
--------------------| -- | --------------------- | -------- |
32 | 5000 | addmod384 | 0.63
32 | 5000 | submod384 | 0.53
32 | 5000 | mulmodmont | 3.0
32 | 50000 | addmod384 | 0.53
32 | 50000 | submod384 | 0.59
32 | 50000 | mulmodmont | 2.38
136 | 5000 | addmod384 | 0.25
136 | 5000 | submod384 | 0.42
136 | 5000 | mulmodmont384 | 2.57
136 | 50000 | addmod384 | 0.27
136 | 50000 | submod384 | 0.16
136 | 50000 | mulmodmont384 | 1.66
192 | 5000 | addmod384 | 0.78
192 | 5000 | submod384 | 0.67
192 | 5000 | mulmodmont384 | 3.0
192 | 50000 | addmod384 | 0.80
192 | 50000 | submod384 | 0.63
192 | 50000 | mulmodmont384 | 2.49
**Table A4.** Cost estimates based on evmone.
#### Worst case
The worst case of the above runtimes with 192 bytes of input:
evm384 opcode | estimated price
--------- | --------
addmod384 | 0.80
submod384 | 0.67
mulmodmont384 | 3.0
**Table A5.** Worst case cost estimates.