# Proto-Danksharding FAQ [TOC] ## What is Danksharding? Danksharding is the new sharding design proposed for Ethereum, which introduces some significant simplifications compared to previous designs. The main difference between all recent Ethereum sharding proposals since ~2020 (both Danksharding and pre-Danksharding) and most non-Ethereum sharding proposals is Ethereum's **[rollup-centric roadmap](https://ethereum-magicians.org/t/a-rollup-centric-ethereum-roadmap/4698)** (see also: [[1]](https://polynya.medium.com/understanding-ethereums-rollup-centric-roadmap-1c60d30c060f) [[2]](https://vitalik.ca/general/2019/12/26/mvb.html) [[3]](https://vitalik.ca/general/2021/01/05/rollup.html)): instead of providing more space for _transactions_, Ethereum sharding provides more space for _blobs of data_, which the Ethereum protocol itself does not attempt to interpret. Verifying a blob simply requires checking that the blob is _[available](https://github.com/ethereum/research/wiki/A-note-on-data-availability-and-erasure-coding)_ - that it can be downloaded from the network. The data space in these blobs is expected to be used by [layer-2 rollup protocols](https://vitalik.ca/general/2021/01/05/rollup.html) that support high-throughput transactions. 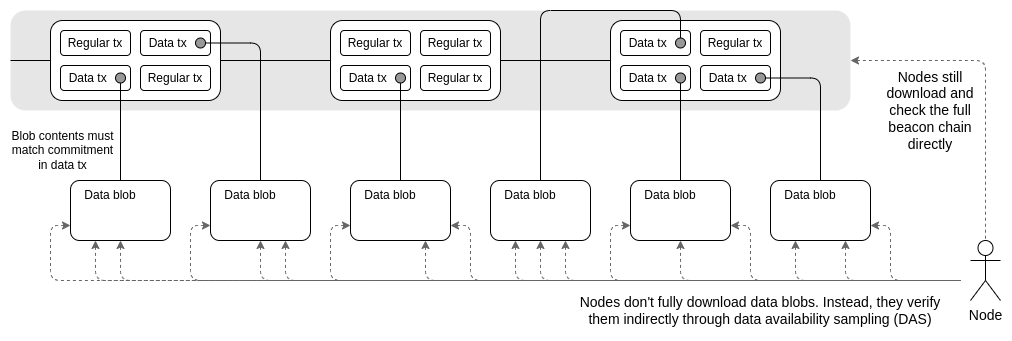<center><br>  </center><br> The main innovation introduced by **[Danksharding](https://notes.ethereum.org/@dankrad/new_sharding)** (see also: [[1]](https://polynya.medium.com/danksharding-36dc0c8067fe) [[2]](https://www.youtube.com/watch?v=e9oudTr5BE4) [[3]](https://github.com/ethereum/consensus-specs/pull/2792)) is the **merged fee market**: instead of there being a fixed number of shards that each have distinct blocks and distinct block proposers, in Danksharding there is only one proposer that chooses all transactions and all data that go into that slot. To avoid this design forcing high system requirements on validators, we introduce **proposer/builder separation (PBS)** (see also: [[1]](https://notes.ethereum.org/@vbuterin/pbs_censorship_resistance) [[2]](https://ethresear.ch/t/two-slot-proposer-builder-separation/10980)): a specialized class of actors called **block builders** bid on the right to choose the contents of the slot, and the proposer need only select the valid header with the highest bid. Only the block builder needs to process the entire block (and even there, it's possible to use third-party decentralized oracle protocols to implement a distributed block builder); all other validators and users can _verify_ the blocks very efficiently through **[data availability sampling](https://hackmd.io/@vbuterin/sharding_proposal)** (remember: the "big" part of the block is just data). ## What is proto-danksharding (aka. EIP-4844)? Proto-danksharding (aka. [EIP-4844](https://eips.ethereum.org/EIPS/eip-4844)) is a proposal to implement most of the logic and "scaffolding" (eg. transaction formats, verification rules) that make up a full Danksharding spec, but not yet actually implementing any sharding. In a proto-danksharding implementation, all validators and users still have to directly validate the availability of the full data. The main feature introduced by proto-danksharding is new transaction type, which we call a **blob-carrying transaction**. A blob-carrying transaction is like a regular transaction, except it also carries an extra piece of data called a **blob**. Blobs are extremely large (~125 kB), and can be much cheaper than similar amounts of calldata. However, blob data is not accessible to EVM execution; the EVM can only view a commitment to the blob. Because validators and clients still have to download full blob contents, data bandwidth in proto-danksharding is targeted to 1 MB per slot instead of the full 16 MB. However, there are nevertheless large scalability gains because this data is not competing with the gas usage of existing Ethereum transactions. ## Why is it OK to add 1 MB data to blocks that everyone has to download, but not to just make calldata 10x cheaper? This has to do with the difference between **average load** and **worst-case load**. Today, we already have a situation where the average block size [is about 90 kB](https://etherscan.io/chart/blocksize) but the theoretical maximum possible block size (if _all_ 30M gas in a block went to calldata) is ~1.8 MB. The Ethereum network has handled blocks approaching the maximum in the past. However, if we simply reduced the calldata gas cost by 10x, then although the _average_ block size would increase to still-acceptable levels, the _worst case_ would become 18 MB, which is far too much for the Ethereum network to handle. The current gas pricing scheme makes it impossible to separate these two factors: the ratio between average load and worst-case load is determined by users' choices of how much gas they spend on calldata vs other resources, which means that gas prices have to be set based on worst-case possibilities, leading to an average load needlessly lower than what the system can handle. But **if we change gas pricing to more explicitly create a [multidimensional fee market](https://ethresear.ch/t/multidimensional-eip-1559/11651), we can avoid the average case / worst case load mismatch**, and include in each block close to the maximum amount of data that we can safely handle. Proto-danksharding and [EIP-4488](https://eips.ethereum.org/EIPS/eip-4488) are two proposals that do exactly that. | | Average case block size | Worst case block size | | - | - | - | | **Status quo** | [85 kB](https://etherscan.io/chart/blocksize) | 1.8 MB | | **EIP-4488** | Unknown; 350 kB if 5x growth in calldata use | 1.4 MB | | **Proto-danksharding** | 1 MB (tunable if desired) | 2 MB | ## How does proto-danksharding (EIP-4844) compare to EIP-4488? **[EIP-4488](https://eips.ethereum.org/EIPS/eip-4488)** is an earlier and simpler attempt to solve the same average case / worst case load mismatch problem. EIP-4488 did this with two simple rules: * Calldata gas cost reduced from 16 gas per byte to 3 gas per byte * A limit of 1 MB per block plus an extra 300 bytes per transaction (theoretical max: ~1.4 MB) The hard limit is the simplest possible way to ensure that the larger increase in average-case load would not also lead to an increase in worst-case load. The reduction in gas cost would greatly increase rollup use, likely increasing average block size to hundreds of kilobytes, but the worst-case possibility of single blocks containing 10 MB would be directly prevented by the hard limit. In fact, the worst-case block size would be _lower_ than it is today (1.4 MB vs 1.8 MB). **Proto-danksharding** instead creates a separate transaction type that can hold cheaper data in large fixed-size blobs, with a limit on how many blobs can be included per block. These blobs are not accessible from the EVM (only commitments to the blobs are), and the blobs are stored by the consensus layer (beacon chain) instead of the execution layer. **The main practical difference between EIP-4488 and proto-danksharding is that EIP-4488 attempts to minimize the changes needed today, whereas proto-danksharding makes a larger number of changes today so that few changes are required in the future to upgrade to full sharding**. Although implementing full sharding (with data availability sampling, etc) is a complex task and remains a complex task after proto-danksharding, this complexity is contained to the consensus layer. Once proto-danksharding is rolled out, execution layer client teams, rollup developers and users need to do no further work to finish the transition to full sharding. Proto-danksharding also separates blob data from calldata, making it easier for clients to store blob data for a shorter period of time. Note that the choice between the two is _not_ an either-or: we could implement EIP-4488 soon and then follow it up with proto-danksharding half a year later. ## What parts of full danksharding does proto-danksharding implement, and what remains to be implemented? Quoting EIP-4844: > The work that is already done in this EIP includes: > > * A new transaction type, of the exact same format that will need to exist in "full sharding" > * _All_ of the execution-layer logic required for full sharding > * _All_ of the execution / consensus cross-verification logic required for full sharding > * Layer separation between `BeaconBlock` verification and data availability sampling blobs > * Most of the `BeaconBlock` logic required for full sharding > * A self-adjusting independent gasprice for blobs. > > The work that remains to be done to get to full sharding includes: > > * A low-degree extension of the `blob_kzgs` in the consensus layer to allow 2D sampling > * An actual implementation of data availability sampling > * PBS (proposer/builder separation), to avoid requiring individual validators to process 32 MB of data in one slot > * Proof of custody or similar in-protocol requirement for each validator to verify a particular part of the sharded data in each block Notice that all of the remaining work is consensus-layer changes, and does not require any additional work from execution client teams, users or rollup developers. ## What about disk space requirements blowing up from all these really big blocks? Both EIP-4488 and proto-danksharding lead to a long-run maximum usage of ~1 MB per slot (12s). This works out to about 2.5 TB per year, a far higher growth rate than Ethereum requires today. **In the case of EIP-4488, solving this requires history expiry ([EIP-4444]((https://eips.ethereum.org/EIPS/eip-4444)))**, where clients are no longer required to store history older than some duration of time (durations from 1 month to 1 year have been proposed). **In the case of proto-danksharding, the consensus layer can implement separate logic to auto-delete the blob data after some time (eg. 30 days)**, regardless of whether or not EIP-4444 is implemented. However, implementing EIP-4444 as soon as possible is highly recommended regardless of what short-term data scaling solution is adopted. Both strategies limit the extra disk load of a consensus client to at most a few hundred gigabytes. **In the long run, adopting some history expiry mechanism is essentially mandatory**: full sharding would add about 40 TB of historical blob data per year, so users could only realistically store a small portion of it for some time. Hence, it's worth setting the expectations about this sooner. ## If data is deleted after 30 days, how would users access older blobs? **The purpose of the Ethereum consensus protocol is not to guarantee storage of all historical data forever. Rather, the purpose is to provide a highly secure real-time bulletin board, and leave room for other decentralized protocols to do longer-term storage**. The bulletin board is there to make sure that the data being published on the board is available long enough that any user who wants that data, or any longer-term protocol backing up the data, has plenty of time to grab the data and import it into their other application or protocol. In general, long-term historical storage is easy. While 2.5 TB per year is too much to demand of regular nodes, it's very manageable for dedicated users: you can buy very big hard drives for [about $20 per terabyte](https://www.amazon.com/Seagate-IronWolf-16TB-Internal-Drive/dp/B07SGGWYC1), well within reach of a hobbyist. Unlike consensus, which has a N/2-of-N [trust model](https://vitalik.ca/general/2020/08/20/trust.html), historical storage has a 1-of-N trust model: you only need one of the storers of the data to be honest. Hence, each piece of historical data only needs to be stored hundreds of times, and not the full set of many thousands of nodes that are doing real-time consensus verification. Some practical ways in which the full history will be stored and made easily accessible include: * **Application-specific protocols (eg. rollups)** can require _their_ nodes to store the portion of history that is relevant to their application. Historical data being lost is not a risk to the protocol, only to individual applications, so it makes sense for applications to take on the burden of storing data relevant to themselves. * Storing historical data in **BitTorrent**, eg. auto-generating and distributing a 7 GB file containing the blob data from the blocks in each day. * **The Ethereum [Portal Network](https://www.ethportal.net/)** (currently under development) can easily be extended to store history. * **Block explorers, API providers and other data services** will likely store the full history. * **Individual hobbyists, and academics doing data analysis**, will likely store the full history. In the latter case, storing history locally provides them significant value as it makes it much easier to directly do calculations on it. * **Third-party indexing protocols like [TheGraph](https://thegraph.com/en/)** will likely store the full history. At much higher levels of history storage (eg. 500 TB per year), the risk that some data will be forgotten becomes higher (and additionally, the data availability verification system becomes more strained). This is likely the true limit of sharded blockchain scalability. However, all current proposed parameters are very far from reaching this point. ## What format is blob data in and how is it committed to? A blob is a vector of 4096 **field elements**, numbers within the range: <small> `0 <= x < 52435875175126190479447740508185965837690552500527637822603658699938581184513` </small> The blob is mathematically treated as representing a degree < 4096 polynomial over the finite field with the above modulus, where the field element at position $i$ in the blob is the evaluation of that polynomial at $\omega^i$. $\omega$ is a constant that satisfies $\omega^{4096} = 1$. A commitment to a blob is a hash of the [KZG commitment](https://dankradfeist.de/ethereum/2020/06/16/kate-polynomial-commitments.html) to the polynomial. From the point of view of implementation, however, it is not important to be concerned with the mathematical details of the polynomial. Instead, there will simply be a vector of elliptic curve points (the **Lagrange-basis trusted setup**), and the KZG commitment to a blob will simply be a linear combination. Quoting code from EIP-4844: ```python def blob_to_kzg(blob: Vector[BLSFieldElement, 4096]) -> KZGCommitment: computed_kzg = bls.Z1 for value, point_kzg in zip(tx.blob, KZG_SETUP_LAGRANGE): assert value < BLS_MODULUS computed_kzg = bls.add( computed_kzg, bls.multiply(point_kzg, value) ) return computed_kzg ``` `BLS_MODULUS` is the above modulus, and `KZG_SETUP_LAGRANGE` is the vector of elliptic curve points that is the Lagrange-basis trusted setup. For implementers, it's reasonable to simply think of this for now as a black-box special-purpose hash function. ## Why use the hash of the KZG instead of the KZG directly? Instead of using the KZG to represent the blob directly, EIP-4844 uses the **versioned hash**: a single 0x01 byte (representing the version) followed by the last 31 bytes of the SHA256 hash of the KZG. This is done for EVM-compatibility and future-compatibility: KZG commitments are 48 bytes whereas the EVM works more naturally with 32 byte values, and if we ever switch from KZG to something else (eg. for quantum-resistance reasons), the commitments can continue to be 32 bytes. ## What are the two precompiles introduced in proto-danksharding? Proto-danksharding introduces two precompiles: the **blob verification precompile** and the **point evaluation precompile**. The **blob verification precompile** is self-explanatory: it takes as input a versioned hash and a blob, and verifies that the provided versioned hash actually is a valid versioned hash for the blob. This precompile is intended to be used by optimistic rollups. Quoting EIP-4844: > **Optimistic rollups** only need to actually provide the underlying data when fraud proofs are being submitted. The fraud proof submission function would require the full contents of the fraudulent blob to be submitted as part of calldata. It would use the blob verification function to verify the data against the versioned hash that was submitted before, and then perform the fraud proof verification on that data as is done today. The **point evaluation precompile** takes as input a versioned hash, an `x` coordinate, a `y` coordinate and a proof (the KZG commitment of the blob and a KZG proof-of-evaluation). It verifies the proof to check that `P(x) = y`, where `P` is the polynomial represented by the blob that has the given versioned hash. This precompile is intended to be used by ZK rollups. Quoting EIP-4844: > **ZK rollups** would provide two commitments to their transaction or state delta data: the kzg in the blob and some commitment using whatever proof system the ZK rollup uses internally. They would use a commitment [proof of equivalence protocol](https://ethresear.ch/t/easy-proof-of-equivalence-between-multiple-polynomial-commitment-schemes-to-the-same-data/8188), using the point evaluation precompile, to prove that the kzg (which the protocol ensures points to available data) and the ZK rollup’s own commitment refer to the same data. Note that most major optimistic rollup designs use a multi-round fraud proof scheme, where the final round takes only a small amount of data. Hence, **optimistic rollups could conceivably also use the point evaluation precompile** instead of the blob verification precompile, and it would be cheaper for them to do so. ## How exactly do ZK rollups work with the KZG commitment efficiently? The "naive" way check a blob in a ZK rollup is to pass the blob data as a private input into the KZG, and do a elliptic curve linear combination (or a pairing) inside the SNARK to verify it. This is wrong and needlessly inefficient. Instead, there is a much easier approach in the case where the ZK rollup is BLS12-381 based, and a moderately easier approach for arbitrary ZK-SNARKs. ### Easy approach (requires rollup to use the BLS12-381 modulus) Suppose $K$ is the KZG commitment, and $B$ is the blob that it is committing to. All ZK-SNARK protocols have some way to import large amounts of data into a proof, and contain some kind of commitment to that data. For example, in [PLONK](https://vitalik.ca/general/2019/09/22/plonk.html), this is the $Q_C$ commitment. All we have to do is prove that $K$ and $Q_C$ are committing to the same data. This can be done with a [proof of equivalence](https://ethresear.ch/t/easy-proof-of-equivalence-between-multiple-polynomial-commitment-schemes-to-the-same-data/8188), which is very simple. Copying from the post: > Suppose you have multiple polynomial commitments $C_1$ ... $C_k$, under $k$ different commitment schemes (eg. Kate, FRI, something bulletproof-based, DARK...), and you want to prove that they all commit to the same polynomial $P$. We can prove this easily: > > Let $z = hash(C_1 .... C_k)$, where we interpret $z$ as an evaluation point at which $P$ can be evaluated. > > Publish openings $O_1 ... O_k$, where $O_i$ is a proof that $C_i(z) = a$ under the i'th commitment scheme. Verify that $a$ is the same number in all cases. A ZK rollup transaction would simply have to have a regular SNARK, as well as a proof of equivalence of this kind to prove that its public data equals the versioned hash. **Note that they should NOT implement the KZG check directly; instead, they should just use the point evaluation precompile** to verify the opening. This ensures future-proofness: if later KZG is replaced with something else, the ZK rollup would be able to continue working with no further issues. ### Moderate approach: works with any ZK-SNARK If the destination ZK-SNARK uses some other modulus, or even is not polynomial-based at all (eg. it uses R1CS), there is a slightly more complicated approach that can prove equivalence. The proof works as follows: 1. Let $P(x)$ be the polynomial encoded by the blob. Make a commitment $Q$ in the ZK-SNARK scheme that encodes the values $v_1 .. v_n$, where $v_i = P(\omega^i)$. 2. Choose $x$ by hashing the commitment of $P$ and $Q$. 3. Prove $P(x)$ with the point evaluation precompile. 4. Use the [barycentric equation](https://hackmd.io/@vbuterin/barycentric_evaluation) $P(x) = \frac{x^N - 1}{N} * \sum_i \frac{v_i * \omega^i}{x - \omega^i}$ to perform the same evaluation inside the ZKP. Verify that the answer is the same as the value proven in (3). (4) will need to be done with mismatched-field arithmetic, but [PLOOKUP](https://eprint.iacr.org/2020/315.pdf)-style techniques can do this with fewer constraints than even an arithmetically-friendly hash function. Note that $\frac{x^N - 1}{N}$ and $\omega^i$ can be precomputed and saved to make the calculation simpler. For a longer description of this protocol, see: https://notes.ethereum.org/@dankrad/kzg_commitments_in_proofs ## What does the KZG trusted setup look like? See: * https://vitalik.ca/general/2022/03/14/trustedsetup.html for a general description of how powers-of-tau trusted setups work * https://github.com/ethereum/research/blob/master/trusted_setup/trusted_setup.py for an example implementation of all of the important trusted-setup-related computations In our case in particular, the current plan is to run in parallel four ceremonies (with different secrets) with sizes $(n_1 = 4096, n_2 = 16)$, $(n_1 = 8192, n_2 = 16)$, $(n_1 = 16384, n_2 = 16)$ and $(n_1 = 32768, n_2 = 16)$. Theoretically, only the first is needed, but running more with larger sizes improves future-proofness by allowing us to increase blob size. We can't _just_ have a larger setup, because we want to be able to have a hard limit on the degree of polynomials that can be validly committed to, and this limit is equal to the blob size. The likely practical way to do this would be to start with the [Filecoin setup](https://filecoin.io/blog/posts/trusted-setup-complete/), and then run a ceremony to extend it. Multiple implementations, including a browser implementation, would allow many people to participate. ## Couldn't we use some other commitment scheme without a trusted setup? Unfortunately, using anything other than KZG (eg. [IPA](https://vitalik.ca/general/2021/11/05/halo.html) or SHA256) would make the sharding roadmap much more difficult. This is for a few reasons: * Non-arithmetic commitments (eg. hash functions) are not compatible with data availability sampling, so if we use such a scheme we would have to change to KZG anyway when we move to full sharding. * IPAs [may be compatible](https://ethresear.ch/t/what-would-it-take-to-do-das-with-inner-product-arguments-ipas/12088) with data availability sampling, but it leads to a much more complex scheme with much weaker properties (eg. self-healing and distributed block building become much harder) * Neither hashes nor IPAs are compatible with a cheap implementation of the point evaluation precompile. Hence, a hash or IPA-based implementation would not be able to effectively benefit ZK rollups or support cheap fraud proofs in multi-round optimistic rollups. * One way to keep data availability sampling and point evaluation but introduce another commitment is to store multiple commitments (eg. KZG and SHA256) per blob. But this has the problem that either (i) we need to add a complicated ZKP proof of equivalence, or (ii) all consensus nodes would need to verify the second commitment, which would require them to download the full data of all blobs (tens of megabytes per slot). Hence, the functionality losses and complexity increases of using anything but KZG are unfortunately much greater than the risks of KZG itself. Additionally, any KZG-related risks are contained: a KZG failure would only affect rollups and other applications depending on blob data, and leave the rest of the system untouched. ## How "complicated" and "new" is KZG? KZG commitments were introduced [in a paper in 2010](https://link.springer.com/chapter/10.1007/978-3-642-17373-8_11), and have been used extensively since ~2019 in [PLONK](https://vitalik.ca/general/2019/09/22/plonk.html)-style ZK-SNARK protocols. However, the underlying math of KZG commitments is a [relatively simple](https://vitalik.ca/general/2022/03/14/trustedsetup.html#what-does-a-powers-of-tau-setup-look-like) piece of arithmetic on top of the underlying math of elliptic curve operations and pairings. The specific curve used is [BLS12-381](https://hackmd.io/@benjaminion/bls12-381), which was generated from the [Barreto-Lynn-Scott family](https://eprint.iacr.org/2002/088.pdf) invented in 2002. Elliptic curve pairings, necessary for verifying KZG commitments, are [very complex math](https://vitalik.ca/general/2017/01/14/exploring_ecp.html), but they were invented in the 1940s and applied to cryptography since the 1990s. By 2001, there were [many proposed cryptographic algorithms](https://crypto.stanford.edu/~dabo/papers/bfibe.pdf) that used pairings. From an implementation complexity point of view, KZG is not significantly harder to implement than IPA: the function for computing the commitment (see [above](#What-format-is-blob-data-in-and-how-is-it-committed-to)) is exactly the same as in the IPA case just with a different set of elliptic curve point constants. The point verification precompile is more complex, as it involves a pairing evaluation, but the math is identical to a part of what is already done in implementations of [EIP-2537 (BLS12-381 precompiles)](https://eips.ethereum.org/EIPS/eip-2537), and very similar to the [bn128 pairing precompile](https://eips.ethereum.org/EIPS/eip-197) (see also: [optimized python implementation](https://github.com/ethereum/py_ecc/blob/master/py_ecc/optimized_bls12_381/optimized_pairing.py)). Hence, there is no complicated "new work" that is required to implement KZG verification. ## What are the different software parts of a proto-danksharding implementation? There are four major components: * **The execution-layer consensus changes** (see [the EIP](https://eips.ethereum.org/EIPS/eip-4844) for details): * New transaction type that contains blobs * Opcode that outputs the i'th blob versioned hash in the current transaction * Blob verification precompile * Point evaluation precompile * **The consensus-layer consensus changes (see [this folder](https://github.com/ethereum/consensus-specs/tree/dev/specs/eip4844) in the repo)**: * List of blob KZGs [in the `BeaconBlockBody`](https://github.com/ethereum/consensus-specs/blob/dev/specs/eip4844/beacon-chain.md#beaconblockbody) * The ["sidecar" mechanism](https://github.com/ethereum/consensus-specs/blob/dev/specs/eip4844/validator.md#is_data_available), where full blob contents are passed along with a separate object from the `BeaconBlock` * [Cross-checking](https://github.com/ethereum/consensus-specs/blob/dev/specs/eip4844/beacon-chain.md#misc) between blob versioned hashes in the execution layer and blob KZGs in the consensus layer * **The mempool** * `BlobTransactionNetworkWrapper` (see Networking section of [the EIP](https://eips.ethereum.org/EIPS/eip-4844)) * More robust anti-DoS protections to compensate for large blob sizes * **Block building logic** * Accept transaction wrappers from the mempool, put transactions into the `ExecutionPayload`, KZGs into the beacon block and bodies in the sidecar * Deal with the two-dimensional fee market Note that for a minimal implementation, we do not need the mempool at all (we can rely on second-layer transaction bundling marketplaces instead), and we only need one client to implement the block building logic. Extensive consensus testing is only required for the execution-layer and consensus-layer consensus changes, which are relatively lightweight. Anything in between such a minimal implementation and a "full" rollout where all clients support block production and the mempool is possible. ## What does the proto-danksharding multidimensional fee market look like? Proto-danksharding introduces a [**multi-dimensional EIP-1559 fee market**](https://ethresear.ch/t/multidimensional-eip-1559/11651), where there are **two resources, gas and blobs, with separate floating gas prices and separate limits**. That is, there are two variables and four constants: | | Target per block | Max per block | Basefee | | - | - | - | - | | **Gas** | 15 million | 30 million | Variable | | **Blob** | 8 | 16 | Variable | The blob fee is charged in gas, but it is a variable amount of gas, which adjusts so that in the long run the average number of blobs per block actually equals the target. The two-dimensional nature means that block builders are going to face a harder problem: instead of simply accepting transactions with the highest priority fee until they either run out of transactions or hit the block gas limit, they would have to simultaneously avoid hitting _two_ different limits. **Here's an example**. Suppose that the gas limit is 70 and the blob limit is 40. The mempool has many transactions, enough to fill the block, of two types (tx gas includes the per-blob gas): * Priority fee 5 per gas, 4 blobs, 4 total gas * Priority fee 3 per gas, 1 blob, 2 total gas A miner that follows the naive "walk down the priority fee" algorithm would fill the entire block with 10 transactions (40 gas) of the first type, and get a revenue of 5 * 40 = 200. Because these 10 transactions fill up the blob limit completely, they would not be able to include any more transactions. But the optimal strategy is to take 3 transactions of the first type and 28 of the second type. This gives you a block with 40 blobs and 68 gas, and 5 * 12 + 3 * 56 = 228 revenue.  Are execution clients going to have to implement complex multidimensional knapsack problem algorithms to optimize their block production now? No, for a few reasons: * **EIP-1559 ensures that most blocks will not hit either limit, so only a few blocks are actually faced with the multidimensional optimization problem**. In the usual case where the mempool does not have enough (sufficient-fee-paying) transactions to hit either limit, any miner could just get the optimal revenue by including _every_ transaction that they see. * **Fairly simple heuristics can come close to optimal in practice**. See [Ansgar's EIP-4488 analysis](https://hackmd.io/@adietrichs/4488-mining-analysis) for some data around this in a similar context. * **Multidimensional pricing is not even the largest source of revenue gains from specialization - MEV is**. Specialized MEV revenue extractable through specialized algorithms from on-chain DEX arbitrage, liquidations, front-running NFT sales, etc is a significant fraction of total "naively extractable revenue" (ie. priority fees): specialized MEV revenue seems to average [around 0.025 ETH per block](https://explore.flashbots.net/), and total priority fees are usually [around 0.1 ETH per block](https://watchtheburn.com/). * **[Proposer/builder separation](https://ethresear.ch/t/two-slot-proposer-builder-separation/10980) is designed around block production being highly specialized anyway**. PBS turns the block building process into an auction, where specialized actors can bid for the privilege of creating a block. Regular validators merely need to accept the highest bid. This was intended to prevent MEV-driven economies of scale from creeping into validator centralization, but it deals with _all_ issues that might make optimal block building harder. For these reasons, the more complicated fee market dynamics do not greatly increase centralization or risks; indeed, the principle [applied more broadly](https://ethresear.ch/t/multidimensional-eip-1559/11651) could actually reduce denial-of-service risk! ## How does the exponential EIP-1559 blob fee adjustment mechanism work? Today's EIP-1559 adjusts the basefee $b$ to achieve a particular target gas use level $t$ as follows: $b_{n+1} = b_n * (1 + \frac{u - t}{8t})$ Where $b_n$ is the current block's basefee, $b_{n+1}$ is the next block's basefee, $t$ is the target and $u$ is the gas used. The goal is that when $u > t$ (so, usage is above the target), the base fee increases, and when $u < t$ the base fee decreases. **The fee adjustment mechanism in proto-danksharding accomplishes the exact same goal of targeting a long-run average usage of $t$, and it works in a very similar way, but it fixes a subtle bug in the EIP 1559 approach**. Suppose, in EIP 1559, we get two blocks, the first with $u = 0$ and the next with $u = 2t$. We get: | Block number | Gas in block |Basefee | | - | - | - | | $k$ | - | $x$ | | $k+1$ | $0$ | $\frac{7}{8} * x$ | | $k+2$ | $2t$ | $\frac{7}{8} * \frac{9}{8} * x = \frac{63}{64} * x$ | Despite average use being equal to $t$, the basefee drops by a factor of $\frac{63}{64}$. So when block space usage varies block by block, the basefee only stabilizes when usage is a little higher than $t$; in practice [apparently about 3% higher](https://app.mipasa.com/featured/Ethereum-s-London-Hard-Fork-Easy-Gains-), though the exact number depends on the variance. Proto-danksharding instead uses a formula based on exponential adjustment: $b_{n+1} = b_n * exp(\frac{u - t}{8t})$ $exp(x)$ is the exponential function $e^x$ where $e \approx 2.71828$. At small $x$ values, $exp(x) \approx 1 + x$. 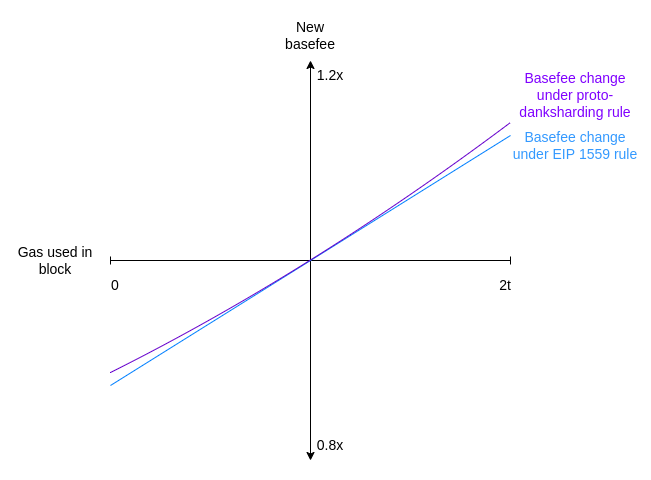In fact, the graphs for proto-danksharding adjustment and EIP-1559 adjustment look _almost exactly the same_:  However, the exponential formula has the convenient property that it is transaction-displacement-independent: the same total usage has the same effect on the basefee, regardless of how it is distributed between different blocks. Copying over the example above, we can see that the exponential formula does in fact fix the issue. | Block number | Gas in block | Basefee using EIP 1559 rule | Basefee using proto-danksharding rule | | - | - | - | - | | $k$ | - | $x$ | $x$ | | $k+1$ | $0$ | $\frac{7}{8} * x$ |$\approx 0.88249 * x$ | | $k+2$ | $2t$ | $\frac{7}{8} * \frac{9}{8} * x = \frac{63}{64} * x$ | $\approx 0.88249 * 1.13314 * x = x$ | We can see why this is true in the general case as follows. The new basefee $b_n$ after a multi-step adjustment can be computed as follows: $b_n\ *\ exp(\frac{u_1 - t}{8t})\ *\ ...\ *\ exp(\frac{u_n - t}{8t})$ But we can re-express this formula a different way: $b_n\ *\ exp(\frac{u_1 - t}{8t})\ *\ ...\ *\ exp(\frac{u_n - t}{8t})$ $= b_n\ *\ exp(\frac{u_1 - t}{8t}\ +\ ...\ +\ \frac{u_n - t}{8t})$ $= b_n\ *\ exp(\frac{u_1\ +\ ...\ +\ u_n - nt}{8t})$ And from here we can see that $b_n$ depends only on the total usage ($u_1 + ... + u_n$), and not how that usage is distributed. **The term $(u_1\ +\ ...\ +\ u_n - nt)$ can be viewed as the _excess_: the difference between the total gas actually used and the total gas _intended_ to be used**. The fact that the current basefee equals $b_0 * exp(\frac{excess}{8t})$ makes it really clear that the excess can't go out of a very narrow range: if the excess goes above $8t * 60$, then the basefee becomes $e^{60}$, which is so absurdly high that no one can pay it, and if it goes below 0 then the resource is basically free and the chain will get spammed until the excess goes back above zero. The adjustment mechanism in proto-danksharding works in exactly these terms: it tracks `actual_total` ($u_1\ +\ ...\ +\ u_n$) and computes `targeted_total` ($nt$), and computes the price as an exponential of the difference. To make the computation simpler, instead of using $e^x$ we use $2^x$; in fact, we use an _approximation_ of $2^x$: the `fake_exponential` function in [the EIP](https://eips.ethereum.org/EIPS/eip-4844). The fake exponential is almost always within 0.3% of the actual value. To prevent long periods of underuse from leading to long periods of 2x full blocks, we add an extra feature: we don't let $excess$ go below zero. If `actual_total` ever goes below `targeted_total`, we just set `actual_total` to equal `targeted_total` instead. This does break transaction order invariance in extreme cases (where the blob gas goes all the way down to zero), but this is an acceptable tradeoff for the added safety. Note also one interesting consequence of this multidimensional market: **when proto-danksharding is first introduced, it's likely to have few users initially, and so for some period of time the cost of a blob will almost certainly be extremely cheap, even if "regular" Ethereum blockchain activity remains expensive**. It is the author's opinion that this fee adjustment mechanism is _better_ than the current approach, and so eventually _all_ parts of the EIP-1559 fee market should switch to using it. For a longer and more detailed explanation, see [Dankrad's post](https://dankradfeist.de/ethereum/2022/03/16/exponential-eip1559.html). ## How does `fake_exponential` work? Here's the code of `fake_exponential` for convenience: ```python def fake_exponential(numerator: int, denominator: int) -> int: cofactor = 2 ** (numerator // denominator) fractional = numerator % denominator return cofactor + ( fractional * cofactor * 2 + (fractional ** 2 * cofactor) // denominator ) // (denominator * 3) ``` Here it the core mechanism re-expressed in math, with rounding removed: $FakeExp(x) = 2^{\lfloor x \rfloor} * Q(x - \lfloor x \rfloor)$ $Q(x) = 1 + \frac{2}{3} * x + \frac{1}{3} * x^2$ The goal is to splice together many instances of $Q(x)$, one shifted and scaled up appropriately for each $[2^k, 2^{k+1}]$ range. $Q(x)$ itself is an approximation of $2^x$ for $0 \le x \le 1$, chosen for the following properties: * Simplicity (it's a quadratic equation) * Correctness on the left edge ($Q(0) = 2^0 = 1$) * Correctness on the right edge ($Q(1) = 2^1 = 2$) * Smooth slope (we ensure $Q'(1) = 2 * Q'(0)$, so that each shifted+scaled copy of $Q$ has the same slope on its right edge as the next copy has on its left edge) The last three requirements give three linear equations in three unknown coefficients, and the above given $Q(x)$ gives the only solution. 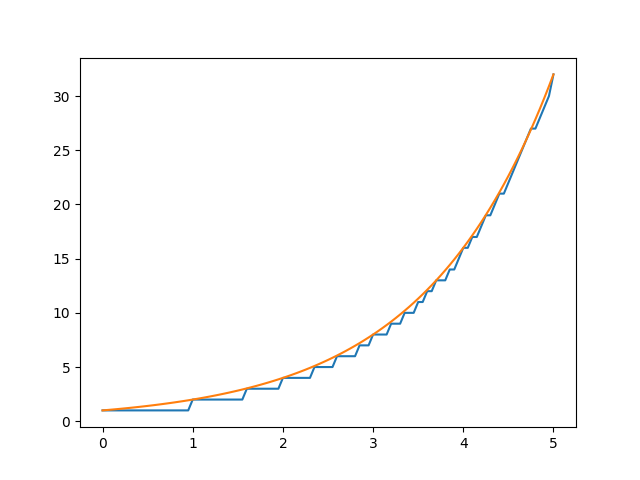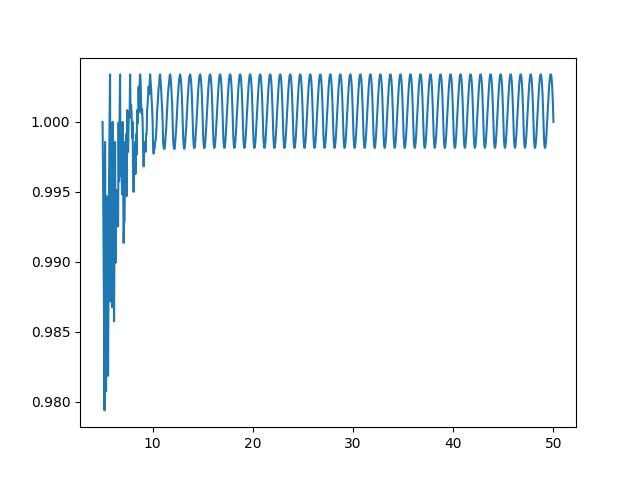The approximation works surprisingly well; for all but the smallest inputs `fake_exponential` gives answers within 0.3% of the actual value of $2^x$: <center><table><tr> <td>  </td><td>  </td> </tr><tr> <td><center> `fake_exponential` (blue) vs actual value of $2^x$ for $0 \le x \le 5$, using step size of 20. </center></td><td><center> `fake_exponential` divided by actual value of $2^x$ for $5 \le x \le 50$, using step size of 20. </center></td> </tr></table></center> ## What are some questions in proto-danksharding that are still being debated? _Note: this section can very easily become out-of-date. Do not trust it to give the latest thought on any particular issue._ * All major optimistic rollups use multi-round proofs, and so they can work with the (much cheaper) point evaluation precompile instead of the blob verification precompile. Anyone who _really_ needs blob verification could implement it themselves: take as input the blob $D$ and the versioned hash $h$, choose $x = hash(D, h)$, use [barycentric evaluation](https://hackmd.io/@vbuterin/barycentric_evaluation) to compute $y = D(x)$ and use the point evaluation precompile to verify $h(x) = y$. Hence, **do we _really_ need the blob verification precompile or could we just remove it and only use point evaluation?** * How well can the chain handle persistent long-term 1 MB+ blocks? If it's too risky, **should the target blob count be reduced at the beginning?** * **Should blobs be priced in gas or in ETH** (that gets burned)? Are there other adjustments to the fee market that should be made? * Should the new transaction type be treated as **a blob or an SSZ object**, in the latter case changing `ExecutionPayload` to a union type? (This is a "more work now" vs "more work later" tradeoff) * Exact details of the **trusted setup implementation** (technically outside the scope of the EIP itself as for implementers the setup is "just a constant", but it still needs to be done).