# Paths toward single-slot finality _Special thanks to Justin Drake, Dankrad Feist, Alex Obadia, Hasu, Anders Elowsson and miscellaneous hackmd anons for feedback and review of various versions of this post._ Today, Ethereum blocks take 64-95 slots (~15 minutes) to finalize. This [was justified](https://notes.ethereum.org/@vbuterin/serenity_design_rationale#Why-32-ETH-validator-sizes) as picking a compromise position on the [decentralization / finality time / overhead tradeoff curve](https://medium.com/@VitalikButerin/parametrizing-casper-the-decentralization-finality-time-overhead-tradeoff-3f2011672735): 15 minutes is not too long and it's comparable to existing exchanges' confirmation times, it allows users to run nodes on regular computers, even with the large number of validators arising from a deposit size of 32 ETH (as opposed to the earlier value [of 1500 ETH](https://eips.ethereum.org/EIPS/eip-1011)). However, there are a lot of good arguments for decreasing the finality time to a single slot. This is a state-of-research post reviewing the roadmap for how to do so. 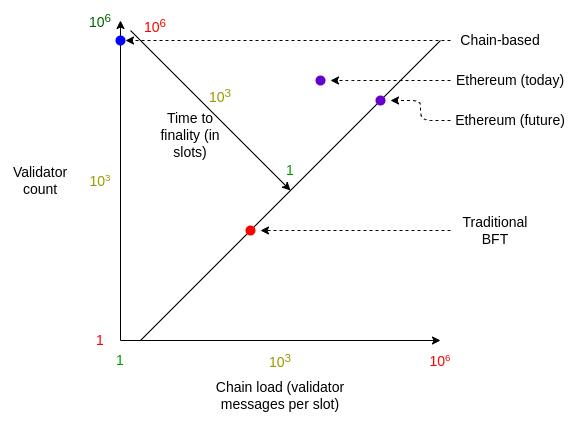## How and why Ethereum staking works today Ethereum's **[LMD GHOST](https://arxiv.org/abs/2003.03052) + [Casper FFG](https://arxiv.org/abs/1710.09437) consensus** is a compromise between the two major styles of consensus popular in proof of stake blockchains: * **Chain-based consensus**, where one message (the **block**) is produced during each slot (a pre-determined interval of time, eg. 12 seconds in Ethereum). Chain-based consensus maximizes the number of participants and minimizes chain load, but easily forks and does not have any notion of finality. * **Traditional BFT consensus**, where each validator makes **two messages ("attestations") per slot** in addition to one validator making a block, and one slot's block gets irreversibly "**finalized**" before the next slot begins. Traditional BFT consensus minimizes time to finality, but at the cost of high chain load and only supporting a small number of participants. Unlike pure chain-based systems, Ethereum's consensus has thousands of attestations voting on the head of the chain in parallel every slot. Every **epoch** (32 slots, or 6.4 min), _all_ active validators get a chance to attest once. After two epochs, the Casper FFG finality gadget finalizes the block, after which point reverting that block requires at least 1/3 of all validators to burn their deposits: **a cost of attack of over ~4 million ETH**. This is unlike pure traditional BFT systems, where finalization happens after one slot. Hence, Ethereum today delivers: * **Medium time to finality** - more than traditional BFT's single slot finality, but not weeks or months or never as offered by chain-based consensus * **Medium chain load** - thousands of messages per slot, but less than the hundreds of thousands that we would have if we used traditional BFT * **Medium node count** - becoming a validator requires 32 ETH: more difficult than in chain-based consensus, where even tiny amounts can participate, but much easier than the very large amounts required in traditional BFT <center><br>  </center><br> The higher level of chain load in Ethereum is enabled by efficiency improvements coming from **[BLS signature aggregation](https://ethresear.ch/t/pragmatic-signature-aggregation-with-bls/2105)**. Thanks to these efficiency gains, **high chain load in messages-per-second terms translates to only medium chain load in terms of data and CPU costs**. BLS signature aggregation works by combining together many signatures into one, such that verifying the combined signature requires only one extra elliptic curve _addition_ (not multiplication) per participant, and an arbitrarily large signature fits into 64 bytes, requiring only 1 extra bit per participant to store who participated. | Signature type | Computation costs per participant | Data costs per participant | | - | - | - | | Schnorr | 2 ECMULs (~ 512 ECADDs) | 48+ bytes | | BLS | 1 ECADD | 1 bit | The combination of the compromise between the chain-based and traditional BFT approaches, with the pure efficiency gains enabled by BLS, leads to the consensus that Ethereum has today. ## So why change it? In the years since the original Ethereum consensus protocol was developed using the above reasoning, we learned one major piece of good news and one major piece of bad news. ### Bad news: hybrid consensus mechanisms actually have many unavoidable problems The largest issues with hybrid consensus, which combines a fork choice to advance slot-by-slot with a finality gadget to finalize blocks later, are: * **User experience**. Most users are not willing to wait 15 minutes for finality. Today, even exchanges frequently consider deposits "finalized" after only 12-20 confirmations (~3-5 min), despite the low security assurance (compared to true PoS finalization) that 12-20 PoW confirmations offer. * **MEV reorgs**. Hybrid consensus retains the fact that short-range reorgs are _possible_, and so still leaves the door open to a hostile near-majority or majority coordinating to reorg the chain for MEV extraction. See [this post](https://www.paradigm.xyz/2021/07/ethereum-reorgs-after-the-merge/) for a more detailed exposition of the argument. * **Interaction bugs**. The "interface" [between Casper FFG finalization and LMD GHOST fork choice](https://arxiv.org/abs/2003.03052) is a source of significant complexity, leading to a number of attacks that have required fairly complicated patches to fix, with more weaknesses being [regularly discovered](https://ethresear.ch/t/balancing-attack-lmd-edition/11853). * **Other protocol complexity**. Hundreds of lines of spec code are spent on maintaining mechanisms such as validator set shuffling. ### Good news: extremely large validator counts are more possible with BLS aggregation than we thought In the past three years, the concrete efficiency of BLS implementations has improved by leaps and bounds, and our knowledge of how to efficiently process and combine large numbers of messages and data has also greatly improved. There are two primary bottlenecks to supporting a huge number of validators with BLS: * **Final validation**: verifying signatures from N validators requires up to N/2 ECADDs to compute the group public key, and it requires N bits (N/8 bytes) of data to store the bitfield of who participated. In practice, these numbers are increased by up to 16x due to the need to have redundant aggregators for [view-merge](https://ethresear.ch/t/view-merge-as-a-replacement-for-proposer-boost/13739). * **Aggregation**: combining together independently-sent signatures from N validators into a combined aggregate signature. This requires a total of at least 96 * N bytes of bandwidth to process, and it requires at least N ECADDs over the (4x more computation-intensive) G2 group, but this can be more easily "sharded" into subnets. Final validation is actually very scalable. A single ECADD can be done in ~500 ns, so 1 million ECADDs would take ~500 ms. The bitfield for 1 million validators would only be 128 kB. The redundancies of view-merge may require verifying up to 16 separate signatures per slot; this increases data requirements to a still-manageable 2 MB (roughly equal to the [EIP-4844](https://eips.ethereum.org/EIPS/eip-4844) max blob data per block and the current max calldata per block), and increases worst-case ECADD cost by ~8x (not 16x due to clever pre-computation tricks). These are both worst-case numbers; in the common case, the 16 aggregators' bitfields would mostly agree, allowing most of the extra cost of having multiple aggregates to be compressed away. Aggregation is more challenging, but also quite feasible. Recent work has greatly improved our understanding of how to aggregate very large numbers of signatures in one slot. The good news is that we have every reason to believe that processing hundreds of thousands of signatures per slot is possible, though more ongoing work is still required to determine and agree on the best solution. **These two facts together mean that the balance of tradeoffs no longer favors an "interior solution" compromising between chain-based and BFT-inspired PoS, and instead favors something much closer to the full-on traditional-BFT route of finalizing each block before starting the next one.** ## What are the key questions we need to solve to implement single slot finality? There are three: 1. **Developing the exact consensus algorithm**. We cannot quite take Tendermint or another existing BFT algorithm as-is, because we highly value maintaining liveness even if $> \frac{1}{3}$ of validators go offline (which traditional BFT does not provide). We need to add on a fork choice, inactivity leak and recovery mechanism to cover this case. Ideally, we achieve maximum safety: $\frac{1}{2} - \epsilon$ fault tolerance when the network is synchronous, and $\frac{1}{3} - \epsilon$ fault tolerance when it is not. 2. **Determining the optimal aggregation strategy**. For as high an $N$ as possible, we want to aggregate and include signatures from $N$ validators into a block, with a level of node overhead that we are willing to accept. 3. **Determining the validator economics**. Even despite aggregation and final validation improvements, single-slot-finality Ethereum may end up supporting a smaller theoretical-maximum validator count than status quo Ethereum. If this count ends up lower than the number of validators who want to participate, how do we limit participation, and what sacrifices do we make? ## What might the exact consensus algorithm look like? As mentioned above, we want a consensus algorithm that follows the Casper FFG + LMD GHOST "finalized chain + optimistic chain" paradigm, where under extreme conditions the optimistic chain can revert, but the finalized chain can never revert. This requires a similar combination of a fork choice and a finality gadget to what we have today, with one key difference: today, we generally have both the fork choice _and_ the finality gadget running, but in a single-slot-finality world, we would have either a fork choice _or_ a finality gadget running: the former would determine the available chain if $< \frac{2}{3}$ of validators are online and honest, and the latter would dominate the fork choice by finalizing blocks if $\frac{2}{3}$ of validators are. Some interaction issues between the fork choice and the consensus do remain in any such design, and it's still important to work through them. Short-term improvements to the existing fork choice (eg. view-merge) may also feed into work on the SSF fork choice. **Exact proposals for algorithms are in-progress; no formal works or writeups have been published yet**. ## What are the issues with developing an optimal aggregation strategy? First, let us look at how aggregation works today. In a single slot, there are $\approx 2^{14}$ validators, which are split into $2^6 = 64$ **committees** each of size $\approx 2^8 = 256$ validators. First, validators from each committee broadcast their signatures in a **p2p subnet** dedicated to that committee. Each committee also has 16 **designated aggregators**, each of which combines together all the signatures that they see into a single aggregate signature (96 bytes + 256-bit bitfield). The designated aggregators publish their aggregates into the **main subnet**. The block proposer then takes the best (meaning, highest total balance of participants) aggregate from each committee, and puts it into their block. With the [view merge](https://ethresear.ch/t/view-merge-as-a-replacement-for-proposer-boost/13739) fork choice patch, they would also add a sidecar object containing the other aggregates; this protects the view merge mechanism from dishonest aggregators as long as at least one aggregator in each committee is still honest.  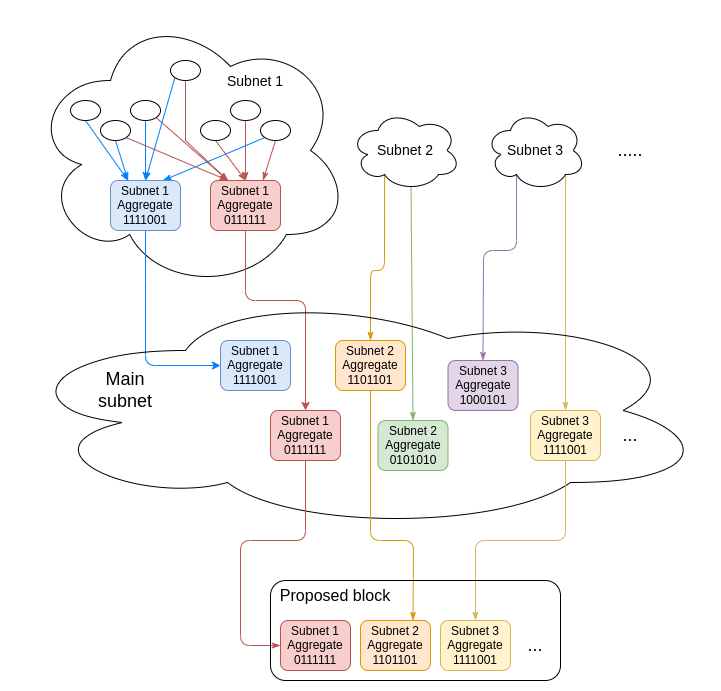If we want to expand this model to single-slot finality, then we need to be able to handle all $2^{19}$ (or however many we have) validators within each slot. This requires one of two sacrifices: * **Increase either validators-per-committee or the committee count**, or both, to accommodate the higher validator count. * **Move to _three-layer_ aggregation**, with two layers of committees. First, signatures would get aggregated into groups of $2^8 = 256$, then groups of eg. $2^{14} = 16384$ and finally the full validator set. The former requires significantly more p2p network load, the latter requires more latency, more risk from a high p2p subnet count, and extra complexity to make sure view merge is protected from malicious aggregators at all levels. Work on analyzing both strategies is actively ongoing. ## What are the issues with validator economics? Today, there are $\approx 2^{19}$ active validators (to be exact, 445,064 at the time of this writing), each of which have contributed 32 ETH to be validators. By the time single-slot finality gets implemented, this may increase to $2^{20}$ or even higher. This leaves us with an important question: **if we can only feasibly process signatures from N validators per slot, but more than N validators want to participate, how do we determine who stays and who goes?** **This is an important issue, as any solution will involve weakening one or more properties of the staking system that are viewed as hard guarantees today**. ### The good news: gains from enabling voluntary validator balance consolidation Because single-slot finality removes any notion of committees (even [danksharding](https://notes.ethereum.org/@vbuterin/proto_danksharding_faq#What-is-Danksharding) does not use fixed-size committees), we no longer need the 32 ETH validator effective balance cap. For p2p network stability reasons, we may still want a much higher cap (eg. 2,048 ETH), but even still, this means that a huge number of validator slots belonging to wealthy users will get consolidated into a much smaller number of validator slots. 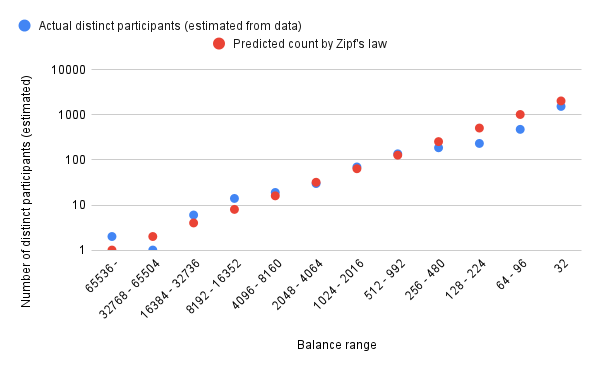We can estimate how much we gain from consolidating wealthy users' validator slots with [Zipf's law](https://en.wikipedia.org/wiki/Zipf%27s_law): the number of stakers who have roughly a particular balance is inversely proportional to that balance (so there are 10x more stakers with 100-200 ETH than there are with 1000-2000 ETH). Using [data from the beacon chain's early history](https://twitter.com/VitalikButerin/status/1335729572633923584), it looks like Zipf's law approximates the distribution quite accurately: <center>  </center> Assuming "pure" Zipf's law, $N$ stakers will have roughly $32 * N * log_2(N)$ ETH and require $N * log_2(N)$ validator slots today. Fitting $2^{25} \approx$ 33.5 million ETH to this, we get 65536 stakers, which consume $2^{20} = 1048576$ validator slots today. Hence, removing the effective balance cap entirely would reduce the number of validator slots we need to process to 65,536, and keeping a cap of 2,048 ETH (up from 32 ETH today) would increase this by only an extra ~1000-2000 validators. This would require only a ~2x improvement in aggregation technology or a ~2x increase in load to be able to handle single-slot finality today! As a side benefit, this also increases fairness for small stakers, because small stakers would be able to stake all of their balance instead of only some fraction of it (eg. someone with 48 ETH today can only stake 2/3 of their ETH). Staking rewards would get automatically re-staked, allowing even small validators to benefit from compounding. In fact, for this reason, increasing the cap to 2,048 ETH may even be a good idea today! However, we still need to handle the exceptional case where either (i) the distribution of validator balances becomes very non-Zipfian, or (ii) wealthy validators decide not to consolidate, or (iii) we get much more than 33 million ETH staking. I see two realistic strategies for handling these cases: **super-committees** and **validator set size capping**. 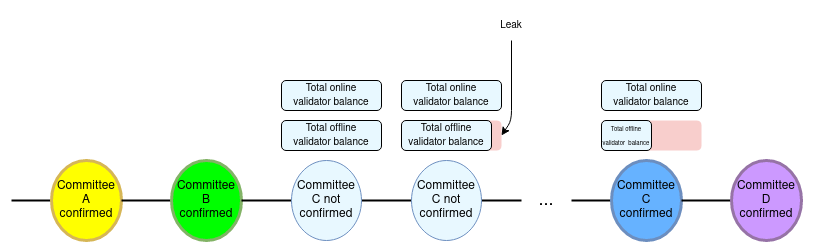## Idea 1: super-committees **Instead of _all_ validators participating in each Casper FFG round, only a medium-sized super-committee of a few tens of thousands participates, allowing each round of consensus to happen within a single slot.** The technical idea was first introduced in [this ethresear.ch post](https://ethresear.ch/t/a-model-for-cumulative-committee-based-finality/10259). The post describes the idea in much more detail, but the core principle is simple: only a medium-sized "super-committee" (eg. 4 million ETH worth) randomly sampled from the full validator set is active at any given time. The committee changes, replacing up to 25% of its members with new randomly chosen validators, every time the chain finalizes. <center>  </center><br> In this strategy, the answer to "who stays and who goes?" is: everyone stays a fraction of the time and goes a fraction of the time. ### How big do the super-committees have to be? This question boils down to a simpler one: how expensive do we need it to be to 51% attack Ethereum? Ideally, the amount of ETH that gets slashed and inactivity-leaked from an attack would be greater than the revenue that can be realistically gained from the attack. The cost of attack should even be high enough to deter or bankrupt powerful attackers that have large outside incentives to break the chain. The question of how much ETH is required to achieve this is inevitably a matter of intuition. Here are some questions we could ask: * Suppose that the Ethereum chain gets 51% attacked and the community needs to spend a few days coordinating an off-chain governance event to recover, but X percent of all ETH gets burned. How large does X need to be for this to be net-good for the Ethereum ecosystem? * Suppose a major exchange gets hacked for millions of ETH, and the attacker deposits the proceeds and gets over 51% of all validators. How many times should they be able to 51% attack the chain before all their stolen money is burned? * Suppose that a 51% attacker starts repeatedly re-orging the chain for only a short time to capture all the MEV. What level of cost per second do we want to impose on the attacker? * [Estimates from Justin Drake](https://www.joincolossus.com/episodes/14242194/drake-ethereum-into-the-ether?tab=transcript) suggest that the cost of _spawn-camp attacking_ Bitcoin today (so, repeatedly 51% attacking until the community changes the PoW algorithm) is around $10 billion, or 1% of the market cap. How many times that level should the cost of _one-time 51% attacking_ Ethereum be? 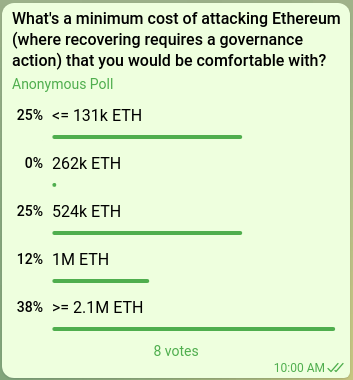<center><br>  <small><i> Internal poll among Ethereum researchers. </i></small> </center> A 1 million ETH cost of attack would imply a super-committee size of 2 million ETH (~65,536 validators) if we focus only on non-latency-dependent 51% attacks, and 3 million ETH (~97,152 validators) if we also include 34% attacks that involve complicated combinations of malicious validators and network manipulation. ### Complexity costs Aside from lowering cost of attack, another major weakness of this scheme is complexity, both complexity of protocol and complexity of analysis. Particularly: * We would need hundreds of lines of spec code to select super-committees and rotate them. * Wealthy validators would distribute their ETH between many validator slots to reduce variance, so we would lose some of the benefit of raising the effective balance cap. * In a temporary high-fees or high-MEV regime, a super-committee may feel the desire to intentionally stall finality to avoid getting rotated out, so that it can keep collecting the fees and MEV. ## Idea 2: validator set size capping We could try to adopt either (or both) of two kinds of caps: * **Capping the total ETH deposited** * **Capping the total validator _count_** Either cap could be implemented either with an **order-based mechanism** (stack or queue) or with **economic mechanisms**. Order-based approaches are highly problematic. To see why, consider two general classes of order-based strategies: * **Oldest validators stay (OVS)**: if the validator set is full no one else can join * **Newest validators stay (NVS)**: if the validator set is full the oldest validators get kicked out Each of these has significant problems. OVS risks turning into an entrenched "dynasty" of early stakers, who cannot leave or else they lose their position. It would also lead to either an MEV auction to join every time a validator leaves, or a very long queue to join the validator set. All of these effects would likely create a significant pressure toward liquid staking pools. NVS, on the other hand, risks creating a permanent MEV auction that would pollute the chain, as validators that get kicked out would want to immediately rejoin, and would fight with genuine new joiners. 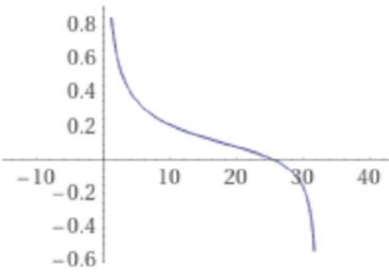### Economic capping of total deposits The alternative is economic capping: if too many validators want to join, penalize _all_ new and existing validators until some give up and leave. A simple approach is to change the validator reward formula from its current $R = \frac{k}{\sqrt{D}}$ to something like: $$R = k * (\frac{1}{\sqrt{D}} - \frac{0.5}{\sqrt{2^{25} - D}})$$ Where $R$ is the reward for well-performing validators (badly-performing validators get some lower reward), and $D$ is the total ETH balance of currently active validators. This curve looks roughly as follows: <center>  </center> On the left side of the curve, validator rewards function as they do today. But as the total deposited ETH grows to many millions, the reward function starts decaying faster, and at ~25 million ETH it drops below zero. Validators might be willing to continue to stake despite zero or negative rewards in the exceptional case where priority fees and MEV are high enough to entice them to validate and compensate for their losses. The reward curve has an asymptote of negative infinity at $2^{25}$ (~33.5 million) ETH, so the validator set size can't grow beyond that point no matter how high these extrinsic rewards are. The strength of this approach is that it completely avoids strange queueing dynamics: no matter where the equilibrium is, it's an equilibrium; the validator set size is what it is because under the current terms, no more validators _want_ to join. The main weakness is [discouragement attack](https://hackingresear.ch/discouragement-attacks/) dynamics near the right side of the curve: an attacker could enter and quickly drive out other validators. But this is a smaller issue than the issues with the other schemes, because it could only happen during exceptional high-MEV situations and because such attacks would be very expensive and require millions of ETH. Another important weakness is that it risks bringing us closer to a future where most validators are "marginal", and large stakers can greatly outcompete small stakers due to their greater tolerance for variance. ### Economic capping of total validator count We can apply the same logic to cap the total validator count, by adding a penalty term proportional to the validator count itself. For example, if we want to impose a cap of $2^{17}$ active validators, we might do: $$R = k * (\frac{1}{\sqrt{D}} - \frac{0.5}{\sqrt{2^{17} - N}})$$ A different approach is to have a **floating minimum balance**: if the validator count exceeds the cap, kick the lowest-balance validator out. The main challenge with a floating minimum balance is mitigating a new kind of griefing attack that emerges: wealthy validators splitting their stake in order to push smaller validators out (and hence increase their reward $R$ because the total deposit amount $D$ decreases). We could mitigate this by adding a fee per validator slot, and target it so that under a Zipfian distribution this is never worth it. However, this would still leave open a potential vulnerability if the distribution becomes very non-Zipfian. **An important issue with all of these proposals is that they change existing guarantees**. Particularly: * Super-committees reduce the total cost of attacking the chain, from 1/3 of total deposits to ~1-2 million ETH. * Economic capping of total deposits or total validator count involves changing the issuance formula, reducing rewards earned by stakers, and increases griefing attacks. * If we add a floating minimum balance, that balance could exceed 32 ETH, violating the present guarantee that anyone with 32 ETH can stake. Careful deliberation is required to determine which of these tradeoffs the community finds most acceptable. ## Summary There are three main questions that need to be researched: 1. **Developing the exact consensus algorithm**, combining together a BFT-inspired consensus algorithm with a fork choice rule in a limited way. 2. **Determining the optimal aggregation strategy**, aggregating signatures from as many validators as possible within one slot. 3. **Determining the validator economics**: answering the question of who stays and who goes if demand for becoming a validator exceeds the system's capacity to process validators. (1) is a specialized academic task, and we know the rough outline of the answer and it is largely a matter of filling in details. That said, accelerating work on (1) and aiming to have specific proposed designs soon is a good idea because it interacts with other lines of research such as proposer/builder separation and SSLE. (2) is also a specialized task, though likely mixed with an unavoidable complexity / efficacy tradeoff. (3) involves the hardest tradeoffs that are not-just-technical and merits engagement from the community.