owned this note
owned this note
Published
Linked with GitHub
# MEV Smoothing
[TOC]
The principles behind the idea are similar to the $l$-smoothed fee mechanism from [Tim Roughgarden's EIP1559 paper](https://timroughgarden.org/papers/eip1559.pdf), which pays the basefee forward rather than burning it, to smooth out the variance in the rewards collected by each proposer. Here we'd try to smooth out variance in MEV, with the goal of having all stakers earning a share of all rewards that is roughly proportional to their stake, just liike with issuance. This is in my opinion the single most impactful consensus-level MEV mitigation that is potentially available to us.
The reason for that is that the size of MEV alone does not make it dangerous, the issue really arises from a combination of size and of variance, both in MEV itself and in proposers' extractive capabilities. If all blocks contained the same MEV and extraction was equally possible for all proposers, MEV would truly just amount to additional issuance, adding to the economic security of the network. Instead, even with democratization of extraction (for example through [separation of builders and proposers](https://ethresear.ch/t/proposer-block-builder-separation-friendly-fee-market-designs/9725)), the high variance of MEV still has many negative externalities:
- **Consensus instability**: not much changes in this respect with democratization of extraction. A block or a span of blocks can still have much more MEV than the following ones, and create incentives for malicious reorgs.
- **Centralization**: democratization is a major mitigation in this respect, but it cannot help with the effect of MEV variance on the distribution of validator rewards, as documented in [this post about MEV in ETH2](https://hackmd.io/@flashbots/mev-in-eth2). MEV morphs this distribution into a long-tailed one, with outsized rewards for a few lucky validators. This favors large staking pools that are able to capture the average rewards of this distribution, because the long tail is included in the average. On the other hand, all but a few validators fall outside of the long tail, and most underperform the average (at a very basic level, mean >> median for a long-tailed distribution). Therefore, pooling stake is more favorable than not doing so, and the larger the pool the better.
- **Weakened contribution to security**: going back to the idea of increased block reward, MEV does increase validator rewards, which should increase the amount of staked ETH and the total economic security of the network. Nonetheless, the decision to stake or not should mostly be driven by predictable rewards, which means that only staking in large pools should be expected to be positively impacted by the long tail of MEV. Given that (by my estimations) the top 1% of FlashBots bundles accounts for around 25% of all rewards, it's then clear that MEV's impact on economic security can be severely weakened by its unpredictability (here I mean just unpredictability in terms of its distribution over the validator set. Unpredictability of the total amount over a long time span is another dimension to this, which we have little control over). On the other end, even the long-tail can be used as an attack subsidy.
## Committee-driven smoothing
There are different ways we can go about trying to achieve some smoothing of MEV over the validator set, more or less complicated depending on the security model that we decide to operate in. I am going to propose a scheme that works in the honest majority model, but I am also going to give some reasons why I think it's reasonable to believe it also works with the stronger assumption of long-term economically rational majority. Moreover, this scheme requires minimal modifications of the existing consensus process.
### Assumptions
Besides the generic assumptions we just discussed, we have to assume the existence of a block content market (as in the builders/proposer post linked above) with two properties:
- **Accessibility**: block headers are equally accessible to all validators, or at least all committee members for the relevant slot. More precisely, all of them have a good chance of timely reception of a block header with a maximal payment or close to it
- **Maximality**: the maximal payment from block headers produced in this market is consistently close enough to the MEV (here in the sense of maximum extracted by any extractor) that no proposer can substantially profit from this difference. For example, if the MEV is 100 and the maximal payment of a block from this block market is 90, a proposer can in principle make a block which extracts 100 and pays out 95, keeping 5 for themselves.
Both properties are not required just for MEV smoothing, but are more generally fundamental to the goals of the proposer/builders separation scheme. Accessibility in that case just means that all proposers can access the block market equally. Maximality means that utilizing blocks from the market is not less profitable than running a private MEV extraction operation, or accessing some other private MEV market. Both properties simply ensure that sophisticated proposers do not have substantially higher profits than unsophisticated proposers.
Given the existence of such a block market, we assume that at attestation time each committee member has their own view of a block with nearly maximal payment, received within the prescribed time window.
### Attestations
Consider committee member $v_i$, with validator index $i$, whose current view is that the payment-maximizing block is $b_i$, making a maximal payment $p_i$. $v_i$ would then attest as follows:
- Attest to a newly proposed block if these conditions are all satisfied:
a) A block has been timely proposed, i.e. it has been received by $v_i$ before a specified deadline (currently 4 seconds after the beginning of the slot)
b) The block extends what in $v_i$'s view is the previous head of the chain
c) The block makes a payment $p$ such that $p \geq p_i$
- Otherwise, attest to the previous head of the chain.
Conditions a) and b) are the same as now, but we add the maximality condition c). Nonetheless, we still have essentially the two options block present vs block absent, except that a proposed block is considered absent if its payment is sub-maximal. The actual attestation rules can be more complicated than this, as we'll see shortly, but the main point is that we can always add condition c) to ensure maximality.
By attesting this way, the committee is essentially trying to coordinate the execution of a tit for tat strategy, punishing non-cooperating proposers to achieve long-term cooperation. For this to be successful, we need that a majority of the published attestations are needed in order for the newly proposed block to become the canonical head of the chain. If they are outnumbered by attestations to the previous head of the chain, the slot should be skipped.
### Fork choice rule
Currently, that is not how the fork choice rule operates. It operates on blocks, not on (block, slot) pairs: attestations to the absence of a block are actually just attestations to the previous head of the chain. This implies that a block that correctly extends the previous head of the chain always becomes the new canonical head of the chain, regardless of how the committee attests. The attestations are immediately relevant only if the proposer has forked the chain.
What we need is instead that a block becomes the new head of the chain only if it receives a majority of the published attestations. Basically, we need a proposed block to be in competition with the empty block. In the diagram below, B is proposed at slot 1 with predecessor A, but it gets fewer attestations than the ones against it, and the canonical chain becomes the one with an empty slot 1.
```graphviz
digraph hierarchy {
nodesep=1.0 // increases the separation between nodes
rankdir=RL //
node [color=black,fontname=Courier,shape=box, width=1] //
edge [color=black, style=solid] //
B->A [color=blue, style=dashed] //
"No B"->A
C->"No B"
"No C"->"No B" [color=blue, style=dashed] //
}
```
More formally, we can think about it with (block, slot) pairs as the competing attestation targets:
```graphviz
digraph hierarchy {
nodesep=1.0 // increases the separation between nodes
rankdir=RL //
node [color=black,fontname=Courier,shape=box, width=1] //
edge [color=black, style=solid] //
"(B,1)"->"(A,0)" [color=blue, style=dashed] //
"(A,1)"->"(A,0)"
"(C,2)"->"(A,1)"
"(A,2)"->"(A,1)" [color=blue, style=dashed] //
}
```
#### Effects of the modified fork choice rule
- Positive: 51% is now actually needed to reorg the chain. Without (block, slot) attestations, there is the possibility to do it with 34%, as discussed by Vitalik [in his talk at reorg.wtf](https://www.crowdcast.io/e/reorg-wtf-summit/register?session=15). The idea is just to not publish a block B built on A, wait for C to be built on A, then release two rounds of attestations for B, so 34+34=68% of one committee, which beats the maximum of 66% that C can get. This is possible because attestations against B currently just count as attestations for A, which do not help C against B, since they are both built on A.
- Negatives:
- the competition between proposed blocks and the empty block can threaten availability under bad network conditions, simply because a majority of attesters do not see the proposed block in time. Besides naturally occuring conditions, this also opens an attack vector to stall the chain, whereas currently it would only cause too much forking.
- Currently, if you propose a block you can do the trick above and fork the next one (with > 1/3). On the other end, if someone else proposes, forking even with > 50% takes time, because your votes "against it" don't count, so you have one block of delay for your votes to start adding up against the canonical chain. If you have 51%, it'll take you 25 blocks to catch up (because with each block you have a 2% advantage over the remaining 49%). If you want to fork in two blocks, you need > 2/3. With the (block, slot) system, you can immediately censor any block.
### A proposal's lifecycle
To give a full picture of the how a block makes its way to the canonical chain, let's focus on a specific version of the builders/proposer separation scheme, specifically Idea 1. The steps are almost the same, except we need to add a deadline for builders' block headers to be considered by attesters in their assessment of the maximal payment. Without one, one could always publish block headers with high payments that are too late to be seen and chosen by the proposer, but still cause attesters to update their view of the maximal payment.
The process would look something like this, with some delay between each step and with attesters being asked to enforce the deadlines in their attestations:
- **Block headers deadline**: builders publish block headers before this time. Attesters accept block headers published after the deadline, but they don't consider them in their view of the maximal payment. This deadline can overlap with the previous slot.
- **Proposal deadline**: the proposer publishes its choice of a block header before this time.
- **Block body deadline**: the chosen builder publishes the body corresponding to the chosen block header before this time
- **Attestation deadline**: at the latest, attesters publish their attestations at this time
Note that this specific version of builders/proposer separation requires its own consensus modifications, with three attestation options:
- Block proposal absent
- Block proposal present but bundle body absent
- Block proposal present and bundle body present
Nonetheless, the changes we need for our smoothing scheme can be simply applied on top, by again equating "block proposal present" with the three conditions a,b,c we identified previously (i.e. adding c)
### Smoothing
Some possibilities are:
- The payment is split equally among all committee members and to the proposer, which would currently be splitting it to about 6250 validators
- The proposer gets some percentage of it, and the rest goes to committee members.
- Either one of the previous options, but committe members only get their share if they attested correctly. The rest is maybe burnt? Redistributive options could be considered, but they create incentives to prevent validators from attesting correctly.
- Same as the last one, but validators only get the percentage of their share corresponding to the correct attestations (similarly to rewards today), to avoid discouragement attacks. The rest is burnt
Here for simplicity I am focusing on the first option, splitting everything equally. We are first going to take a look at the distribution of rewards under the proposer-takes-all status quo, and then at how it would change under this specific smoothing mechanism.
#### No smoothing
To get some idea of the long-term distribution of rewards over the validator set, I considered 200k validators and for each I independently simulated their rewards over a certain span of blocks, by simulating a proposer assignment for them and then giving them the whole miner reward from FlashBots bundles in the block, if there was any. As for the blocks, I started with a dataset of 900k blocks, which span about 4 months, and then replicated 10 times, to have a longer term picture of the rewards. In first plot is the resulting distribution of validator's APRs from MEV only, assuming a starting deposit of 32 ETH for all of them. The second plot shows percentages $p$ versus the $p^{th}$-percentile of the validator APRs, meaning the minimum APR to be in the top $p$% of validators for MEV revenue. The last three marked points are for $p = 95, 98, 99$
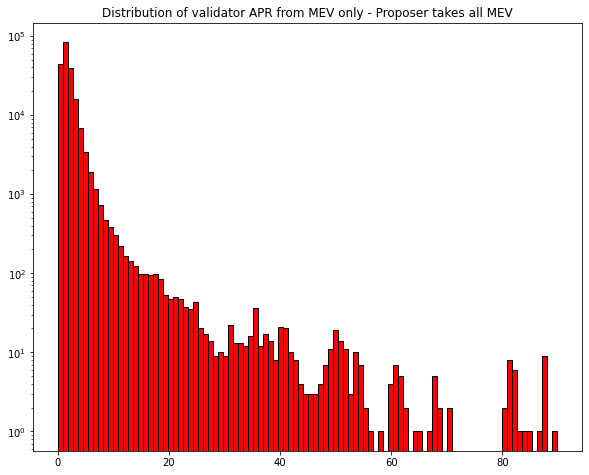
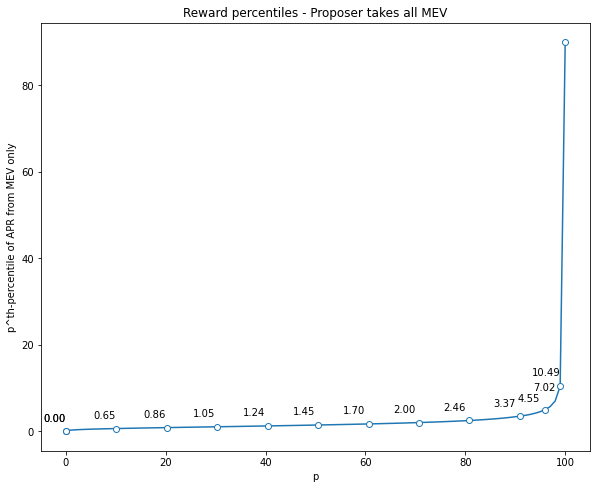
Clearly, the long-tail of MEV extends to validator profits, even over a fairly long period of time such as the one considered. The mean APR is about 1.97%, 36% higher than the median, which is around 1.45 (corresponding to $p = 50$). Moreover, the mean is roughly the $70^{th}$ percentile. This means that 70% of all validators earn less than the mean, and thus less than any sufficiently large staking pool. Therefore, 70% of all solo validators and small staking pools would be less profitable than large staking pools, and this is assuming full democratization of extraction already! It's also worthwhile to note that considering even longer periods of time does not fix this, because of the path dependence of validator profits, due to compounding (assuming that undeperforming validators don't just choose to join larger pools).
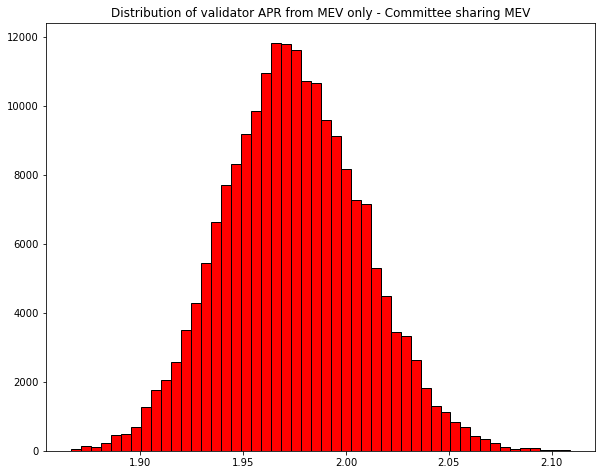
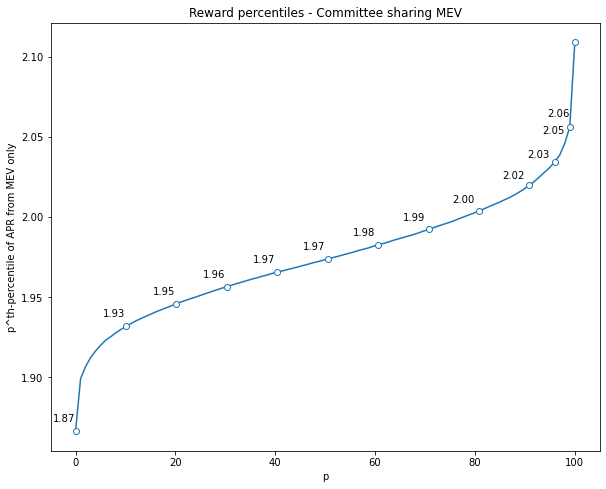
#### Committee-based smoothing
I again simulated profits independently for each validator. A validator gets assigned to one committee per epoch, and gets $\frac{1}{6250}$ of the FlashBots bundles' rewards for the corresponding block, if any. The proposed scheme leads to a fairly equitable distribution of rewards: the most unlucky get about 11% less than the luckiest, and most of the mass is concentrated in a much smaller range. For example, 80% of the mass is between 1.93 and 2.02, a range smaller than 5% of the maximum. Moreover, the distribution is roughly symmetrical around the mean. Such a distribution nullifies the advantage of concentrated stake: there's no long tail, and thus being guaranteed to achieve average rewards is not a big advantage anymore.
## Security
One immediate worry when introducing another aspect to the attestation process is whether or not an adversary can attempt to manipulate attesters' views to produce undesirable outcomes. In particular, let's consider how a committee member's view of the maximal payment can differ from the real one:
- **View > Reality**: without the block headers deadline it is definitely possible to execute an attack using ideas from [this post](https://ethresear.ch/t/attacking-gasper-without-adversarial-network-delay/10187), by releasing a block header with a high payment at a time such that more than 50% of the committee is going to see it in time but the proposer won't, which would cause the block to be rejected.
With a deadline for block headers which is sufficiently in advance of the proposal time, this attack vector is no longer feasible and the ability to delay messages to the proposer is required. There's also a high cost of failure, because the proposer seeing the header in time would lead to having to make the very high promised payment.
Finally, even an adversary that is able to target specific proposers and cause their incoming messages to be delayed would be unable to execute such an attack if the proposer were to be chosen through a [single secret leader election](https://www.reddit.com/r/ethereum/comments/m9j5cy/single_secret_leader_election_protocols/)
- **View < Reality**: attesters whose view of the maximal payment is lower than what it should be will anyway always attest correctly when the proposer is honest. The only mistake they can make is attesting to a sub-optimal block. For a block to be sub-optimal, by definition there has to be a block header which offers a higher payment, because we define optimality through the block content market. That also means that there is a builder who made this maximal block and wants to see it published, and is therefore interested in having as many committee members as possible receiving it in time, thereby preventing competing sub-optimal blocks from being viable choices. We rely on the self-interest of such builders to make sure that committee members don't have a sub-optimal view of the payment, at least as long as the adversary does not have too much control over network delays.
Therefore, the main concern we have is not about potential manipulations of the views of committee members, but about whether well-informed committee members will prevent sub-optimal proposals from becoming canonical, i.e. whether a majority of committee members will be honest. We are going to focus on this aspect, and consider how it interacts with our usual security models.
### Honest Majority Model
Sampling allows us to transfer the honest majority assumption from the whole validator set to a committee. More precisely, with overwhelming probability we have an honest majority in a committee if we have sufficiently more than 50% honest in the whole validator set. For details and precise figures, see [this post](https://www.paradigm.xyz/2021/07/ethereum-reorgs-after-the-merge/).
Given our assumptions on the block content market and the transferability of the honest majority assumption, a committee should with high probability have an honest majority of validators which have a correct view of the current maximal payment, i.e. of validators that have the necessary information to vote correctly and will choose to do so. To be more concrete, let's quantify this a bit. Let ```p``` be the fraction of validators which is honest, and let ```q``` be the minimum fraction of committee members which will see a maximal block header in time, given the way block headers from the block content market propagate in the network. Finally, let ```n``` be the committee size. We want ``` > n/2``` of the committee members to be honest and to have received the necessary information to vote correctly, which means we need ``` > n/2/q``` honest committee members. ```1 - binomial_cdf(n/2/q, n, p) ``` gives us precisely the probability of this, and in the table below there's some sample values, for various ```p,q``` and with ```n = 6250```.
|```p``` | ```q``` | ```1 - binomial_cdf(n/2/q, n, p)``` |
|---------|---------|:-----------------:|
| 0.57 | 0.9 | 0.989 |
| 0.64 | 0.8 | > 0.99 |
| 0.73 | 0.7 | > 0.99 |
| 0.58 | 0.9 | > 0.9999 |
| 0.65 | 0.8 | > 0.9999 |
| 0.74 | 0.7 | > 0.9999 |
| 0.59 | 0.9 | > 0.9999999 |
| 0.66 | 0.8 | > 0.9999999 |
| 0.75 | 0.7 | > 0.9999999 |
You can check these or calculate others by running the following code in Python and changing ```n,p,q```:
```python
from scipy.stats import binom
n = 6250
p = 0.58
q = 0.9
1 - binom.cdf(n/2/q, n, p)
```
No matter how much we increase ```n```, the minimum required fraction of honest nodes ```p``` is mostly controlled by ```q```, because we always need ```p > 0.5/q``` to have a high probability of success: with ```p <= q/2``` we have at best even odds. ```n``` only controls how much higher than ```0.5/q``` we need ```p``` to be in order for the probability to be as high as we desire, which already for ```n = 6250``` is not very far, on the order of 1%. Here is a plot of these minimum values of ```p``` for ```q in [0.5, 1]```.
As we could already see from the table, we need at least```q > 0.75```, or we are forced to assume ```p > 2/3```. In reality, we want to assume much less about ```p```, possibly not much more than we already do for the current fork choice, which is a bit more than honest majority. Moreover, assuming a smaller ```p``` means we have a cushion against attacks, for example against network attacks which increase ```q```. The question is then if it is possible to achieve fairly high values of ```q```, possibly around 90%, without increasing the blocktime at all, or at least not by much. Moreover, $q$ needs to be fairly resistant to p2p layer attacks.
Looking at ethstats.net, we see that the block propagation time to reach 90% of this subsection of the network is around 2 seconds, and around 1 second to reach 80%. The time to reach the same fractions of a committee should be even lower, since the committee communicates with its own subnet.
### Long-term economically rational majority
A more desirable assumption to make is that a majority of validators are rational economic actors, with a long-term perspective, as that is already the core security assumption of Ethereum, like most cryptosystems. I won't try to formally define this assumption and prove something, and I'll instead just give some reasons why I think this scheme is long-term incentive compatible:
- As already explored, the long-term result of correctly participating in this scheme is that MEV is more or less evenly distributed, much more so than currently. For sufficiently large staking pools, this is no different than the status quo, because they already achieve the mean with overwhelming probability (if you don't believe that FlashBots sufficiently democratizes MEV, you can think of what the status quo would be after implementing proposer/builders separation, so that all proposers have roughly the same earning potential. It is anyway required for this scheme). For everyone else, this is better than the status quo, because they are likely to earn more than before, though they sacrifice some low-proability higher upside.
- Consider the single-block game between the proposer and the commitee, where the latter is seen as a single player and the proposer moves first. Defecting means not following the protocol. For the proposer, that is proposing a block which does not make a nearly maximal payment, and instead gives them an undue portion of the MEV. For the committee, that is accepting such a non-maximal block, or failing to accept a maximal one. Here's the payoff matrix for this game:
| | Proposer is honest| Proposer defects |
|-------------------------|:-----------------:|-----------------:|
|**Committee is honest** | (1,1) | (0, 0) |
|**Committee defects** | (0,0) | (0.5,2) |
In this single-block game, the dominant strategy for the proposer is to always defect, because the committee always prefers to get something rather than nothing, i.e. to cooperate. On the other hand, in the repeated form of the game the committee can employ a tit for tat strategy, which corresponds to voting honestly and punishing non-complying proposers. In the long term, this should ensure a cooperative equilibrium. Moreover, as we'll see in a later section about short-term considerations, committee members from large pools have a very different payoff matrix in which the payoff for defecting with the proposer is very low or even negative.
- This game is of course very simplified. In reality, the committee is not one entity, and actually some of its validators will often share interests with the proposer (at least anytime in which the proposer belongs to a sufficiently large staking pool, which happens proportionally to the stake that is held in such pools). Moreover, a validator that's a committee member for one block will later be a proposer for a different block, so players really play both sides. Nonetheless, playing a proposer-friendly long-term strategy is just an attempt to keep the status quo, which as already mentioned does not particularly benefit anyone in terms of rewards. Large pools do benefit from the status quo in that their ability to achieve average rewards gives them an edge in attracting stake, but on the other end fostering staking decentralization can be a net-positive for the whole Ethereum ecosystem and increase the total value of the stake that pools compete for. Moreover, there's a clear reputational cost that comes from subverting the protocol in an easily attributable way, especially for large pools and especially when it comes to a mechanism that's common good-oriented.
#### Beating (0.5, 2) with a simultaneous game
The single-block game theory is made even worse by the fact that the proposer moves first, meaning that they publish their block and only then the committee makes their choice. This simply means that past committee moves are not nearly as relevant to the proposer as they would be in a repeated simultaneous game. In such a game, a long stretch of cooperation (or at least of committee members sticking to the tit for tat strategy) would solidify it as an equilibrium, because an unannounced defection by the proposer would almost certainly be unsuccessful.
In this game instead, the committee knows about the defection before moving, and has the chance to adapt its strategy, for example in response to a block with an unusually high amount of MEV. Thus, proposer can successfully defect even after a long span of coordination. The question is then, can we turn this game into a simultaneous one?
We cannot directly do that, because the committee members should not attest before the deadline for the proposer to publish a block. What we can do is ask committee members to make a commitment which binds their future attesting options, for example by punishing violations with slashing. They can commit to the minimum payment that they would be willing to accept given current information: $v_i$ commits to $p_i$, with $p_i$ being their current view of a maximal payment. As their view of the maximal payment changes, committee members can raise their payment threshold, but what's important is that the commitment prevents them from lowering it, lest they be slashed.
The commitments don't need to go on-chain unless violated, as there's perhaps no need for an incentive system for them. While they restrict a committee member's options, it is a self-imposed restriction which in the long-term serves to further discourage defecting proposers, as 51% of published commitments can suffice to establish a high floor for a block's payment.
### Short-term considerations
#### Payoff for committee's defection
The short-term payoff for defecting when the proposer defects is not much in absolute terms, even for outlier blocks in the long tail of MEV rewards. Per validator, even a block with 100 ETH of MEV is only worth around 1/60 ETH (with the current committee size), at the moment around 50$. More importantly, it is only 0.05% of a validator's deposit. While that's obviously not a negligible amount for a single block, it is hardly a compelling reason to break from the long-term strategy. Moreover, the situation is even more favorable when we look at large (and even not so large) validator pools (regardless of whether or not they are staking pools or a single operator with many validators, as long as they share rewards). In fact, those are statistically well-represented in each committee, meaning that each committee has a roughly equal percentage of validators from the pool, i.e. their percentage in the whole validator set. Given this, we can see that the payoffs for validator pools are not additive, i.e. the payoff for defecting for a validator pool with $n$ validators is not $n$ times the payoff for a single validator. The short-term payoff for defecting might even be negative for a large pool.
This is best seen by example: say the max revenue at a slot is 100 ETH, but the proposer wants to keep 50, and thus proposes a block with 50 ETH of shareable revenue. If a majority of the committee votes honestly, the block does not become the new head of the canonical chain. In the next slot, an honest proposer will _at least_ propose a block with 100 ETH of shareable revenue, possibly more if further opportunities have been found, the tx order has been further optimized or simply if the block can be filled more than it previously could (more fees, but more importantly more extraction opportunities). A validator pool with 10% of the stake will have 10% of validators in both committees, and thus will get at least 10 ETH, whereas they would have gotten 5 ETH if the last block had been accepted. It is true that then there would have been a different new block, with its own reward, but I think that a general principle is that MEV does not disappear just because some slots are missed. If they are, later blocks will be more full, contain more extraction and contain more normal transactions which create more future extractive opportunities. If you are a pool large enough to have roughly the same percentage in every committee, you don't care when extraction is done, just that it is eventually, and *that it is maximally shared with you*, which does not happen if you accept defection from proposers. Depending on how much of the stake is distributed in sufficiently large pools, this might mean that a large part of the committee, maybe even a majority, does not gain anything from defecting after a proposer has defected, or even loses something.
## Consensus stability
Both the current fork-choice rule and the one proposed for this scheme are vulnerable to 51% attacks, with the only difference being that in this scheme a 51% coalition can immediately vote down any minority block, whereas currently it takes some time to convince the minority to join the majority chain (which is necessary to eventually achieve finality). Therefore, when comparing with the status quo we should only worry about consensus instability created by adaptive adversaries which do not have control of 51% of the stake, but can try to achieve such control over specific committees.
Currently, a committee does not get value from the content of a block, but just from coordinating the consensus process. Thus, no one outside of the proposer (and whatever amount of stake they represent) has a reason to do anything to steal MEV by forking. Stealing requires the proposer’s coalition to bribe the rest, and without network attacks the total adversarial percentage in the two committees (including bribed members) has to add up to 2/3 of them (so votes go like 1/3 + 1/3, and 0 + 2/3). On the other end, in this scheme controlling 51% of both committees is enough, because the first block can now directly be skipped, and committee members can have their own incentives to try to fork to steal MEV, because they share the benefits. Nonetheless, the situation is still arguably much better:
- Crucially, proposers from large staking pools have no incentive to fork to steal MEV, because they control about the same percentage of every committee, and thus get about the same percentage of each block's rewards (within very tight bounds, even for proposers controlling only a single-digit percentage of the stake). Since large pools are the most powerful actors, and are potentially able to coordinate, disincentivizing them from attacks is arguably the single most important defense.
- If the proposer is a solo validator or anyway a small staker, they might want to capture a share of the previous block’s rewards, because they didn't receive any of it. On the other end, a staker that’s small enough to not have participated in the rewards meaningfully is very ill-equipped to successfully fork. They essentially have no committee power of their own, and would need to convince everyone else. Pools are especially hard to convince, for the same reason why they don't have a reason to fork, and it's hard to imagine forking without the support of any large concentration of stake. Lots of other small stakers might have incentives to fork, but it’s hard to imagine adaptively coordinating a large coalition of small stakers, especially one large enough to make this work.
## Censorship resistance
The block content market could be very centralized, and it seems likely it will be. Either way, we have no control over whether that is the case. Censorship resistance would then heavily rely on the assumption that altruistic proposers would step up and utilize their discretion in choosing block headers to combat censorship when needed, for example by making their own block. This is not possible with MEV smoothing, because MEV maximization is enforced, and we therefore need to explore other solutions.
Before doing so, let's go over some problems with the assumption we just mentioned, which the builders/proposer separation scheme relies on. Rather than just try to replace the censorship-resistance mechanism with an equivalently problematic one, we'll later argue that MEV smoothing can be used to create a much better one.
### Centralization risks of builders/proposer separation
- We don't want to require proposers to be able to make their own block, including execution. As discussed in this great [post about statelessness](https://dankradfeist.de/ethereum/2021/02/14/why-stateless.html), we eventually want validators to have much lighter hardware and bandwidth requirement and to quickly be able to switch between shards, i.e. to be stateless clients. This is incompatible with proposing in the traditional sense, which requires having the full state in order to execute transactions. Ideally, we wouldn't want to restrict proposing to powerful nodes either, *especially if we rely on proposers for censorship resistance*. The builders/proposer separation allows us to avoid doing so, by outsourcing block making, and it seems like a property that it would be nice to preserve.
- What we require of such proposers is self-harming altruism, because making their own blocks would entail not maximizing MEV. Given that the main goal of builders/proposer separation is allowing unsophisticated proposers to stay unsophisticated, the missed profits might be substantial. It is especially so when we think of solo validators, since they expect to propose only a few dozens blocks a year, and which are probably the staking demographic that's likeliest to be common-good oriented.
- There is no clear attribution of responsibility: there is always going to be some degree of arbitrariness in deciding when a certain threshold of censorship is crossed, and thus in determining who should step up to take care of it. Even for well-intentioned proposer, what's the harm in letting the next proposer take the loss to deal with it? Only the most altruistic proposers should be expected to take on this responsibility, meaning we end up penalizing a strongly altruistic minority, quite opposed to the goals of democratization.
Note that there's one common point between this problem and the problem posed by exploitative MEV: asking altruistic proposers to not extract exploitative MEV means disadvantaging them relative to others. In the case of censorship this might not seem to be as much of a concern because it is currently not a big problem, and giving up some profits to resist very rare bouts of censorship is not as impactful as consistently giving up profits by refusing to extract exploitative MEV. On the other end, censorship is rare because the network is very censorship resistant, and we are now making the incentive compatibility of censorship resistance conditional on there not being too much censorship.
### Leaving some inclusion powers to proposers
The first point of criticism can be fairly easily dealt with: after all, censorship resistance does not require proposers to make blocks, or even to order transactions, but only to select at least some of the included transactions. In other words, what we really want is to leave some transaction inclusion power to proposers. Unfortunately, the remaining problems don't go away if we restrict our demands to inclusion powers. The reason is simply that optimizing inclusion is part of maximally extracting MEV. Expecting proposers to use their inclusion power altruistically falls in the same pitfalls we already explored: we'd expect most proposers to anyway give up this power to builders, in order to maximize profits, and only the most altruistic proposers to use it against censorship, paying an unfair price for their altruism.
With MEV smoothing, allowing proposers to impose restrictions which reduce the MEV extracted is not harmful to the purposes of democratization, _as long as these restrictions do not allow the proposer to beat the block content market_. When that's not the case, they don't impact the relative gains of the proposer in comparison to other stakers: the proposer does not get anything out of these powers, and the lost income due to the reduction in extracted MEV (compared to unrestricted maximization) is shared by everybody.
As a non-example, allowing the proposer to have full control over inclusion violates the above requirement, because the proposer can make sure that any extractive activity will only benefit them, regardless of the ordering of transactions, and can therefore produce a more profitable block than any other builder.
If we only give proposers control over a small enough portion of the gas limit, I think we can satisfy this property. Even if proposers attempt to use their limited inclusion powers for MEV extraction, they have no way of preventing generalized frontrunning of their extraction attempts, since builders have control of ordering and are able to insert their own extractive transactions. Failed extraction attempts are even costly, and so reduce a proposer's ability to build a maximal block. What they can profit from is being able to give instant inclusion guarantees, but I don't think that that's going to be particularly lucrative: normal transactions wouldn't want to pay much more than the basefee just for inclusion, and very urgent transactions can already get very good inclusion guarantees by paying a high tip, without needing to figure out which proposer can give them an instant inclusion guarantee, and how to pay them.
The construction can be as follows: when publishing their choice of a block header, a proposer chooses also a set of transactions to be included in the next block (or any successive block that has the chosen block header as predecessor), consuming up to a certain predefined portion of the gas limit. A builder tries to produce a maximally profitable block including the transactions chosen by the proposer of the block it is building on, and they're allowed to use any leftover gas and have full control over the ordering of all transactions.
In practice it should look like this:
1. At slot n, the proposer chooses a header and together with that publishes a list of transactions and a hash of the list. The sum of the gas limits of the transactions needs to be less than some predefined fraction of the current gas limit.
2. The chosen builder for slot n publishes the block.
3. Before slot n+1, builders make blocks built on the one from step 2 and containing all transactions chosen by the previous proposer, plus any others up to the gas limit, in any order. They include the signed hash and a list containing the indices of the transactions chosen by the previous proposer. For example, the list [10, 25] indicates that the first transaction in the list from step 1 has been included at index 10 in this block, and the second one at index 25. Finally, they publish the headers.
4. The proposer of slot n+1 chooses a block header, together with the list of transactions for the next block.
5. The chosen builder for slot n+1 publishes the block
Together with the usual validity conditions of a block, we require that the hash of the list of transactions restricted to the given indices matches the one provided by the proposer, which of course has to be correctly signed.
#### Incentive compatibility
- **Couldn't a builder bribe a proposer to choose transactions which they think will maximize MEV, reducing the effectiveness of MEV smoothing?**
They could, but does it make sense? The chosen set of transactions cannot be withheld by the proposer, because it needs to be published with the block header, so any builder is able to work with it to make a maximally profitable block. The builder paying this bribe is then far from guaranteed to win. Actually, paying the bribe requires them to try to bid less than the maximum to stay profitable, so you'd normally expect them to lose. Why pay at all then? Yes, you can create conditions for a more profitable block, but it doesn't guarantee that you will reap the benefits. The key here is essentially just the property we required in the last section, which is that the power given to the proposer cannot be used to beat the block content market.
One drawback is that this does require a somewhat competitive block market, where paying a large bribe to the proposer is infeasible because it creates a strong competitive advantage for all other builders.
- **Even without being bribed, why wouldn't a proposer not try to do inclusion in a profit-maximizing way, i.e. choosing transactions which allow MEV to be maximized?**
If they are not paid for it (which would let them earn more than others), whether or not they do so is not important! Sure, many proposers might decide to optimize their use of inclusion power, for example by letting builders tell them which transactions to include in order to allow for maximally profitable blocks to be built, or to avoid having to maintain a mempool. The point is, they maximize everyone's profits rather than only their own, and thus get no relative advantage from it!
### Sustainable altruism
If proposers can freely decide to use their inclusion powers to maximize profits, are we not still relying on proposers to be altruistic for censorship resistance? What have we gained in terms of censorship resistance?
We are indeed still relying on altruism, but on a much much weaker notion of altruism, which requires no relative losses compared to other stakers and minimal absolute losses, and moreover whose impact on the altruist's profits is proportional to their stake. Let's look at why, and compare with the plain builders/proposer separation scheme:
- A proposer choosing not to follow a profit-maximizing inclusion strategy (for example to privilege censorship resistance) does not miss any more profits because of this than anyone else, relative to their stake. In other words, all missed profits are shared by everyone, proportionally to stake [^bignote1], so democratization through smoothing is preserved. On the contrary, in the plain builders/proposer scheme any validator choosing to follow a sub-optimal strategy earns less than the ones who don't, threatening the goals of democratization.
- The total losses incurred by a node operator which follows a sub-optimal inclusion strategy are a fraction of what they are in the plain builders/proposer scheme. For operators controlling a sufficiently high number of validators, this fraction is precisely the fraction of stake they control, so a solo validator gets the greatest reduction in total losses.
- The percentage of missed profits that such an operator incurs because of their altruism is proportional to their stake. For example, an operator with 10% of the stake can at most incur a 10% reduction in their profits, but an operator with 1% of the stake can incur at most a 1% reduction. Thus, a smaller operator incurs smaller losses for each validator that they decide to use altruistically. The reason is simply that each validator that is used altruistically reduces the profits of every other validator, and so controlling more validators compounds the missed profits. For a solo validator, about 99.9995% of profits are independent of their choices, so being altruistic can at worst mean missing 0.0005% of the theoretical maximum profits (about $\frac{1}{200000}$, and decreasing as the amount of stake ETH grows). This is fundamentally different from what happens in the plain builders/proposer separation scheme, because there each validator is responsible for 100% of their profits, so the maximum theoretical missed profits are also 100%.
To make it more concrete, say I have 10% of the stake and I do inclusion in a way which is not profit maximizing, and somehow it always makes blocks half as profitable as they could be. To simplify, say all other blocks have 20 units of MEV and mine have 10. Since I propose one in 10 blocks and get about 10% of any block's MEV, whether the block is mine or not, overall I get 20x0.1x0.9 + 10x0.1x0.1 = 1.9 per block, a loss of 5% from the theoretical max 2 = 20x0.1. Now suppose I have 1% of the stake and I follow the same strategy. My EV is 20x0.01x0.99 + 10x0.01x0.01 = 0.199, a loss of 0.5% from the theoretical max 0.2 = 20x0.01
Generally, consider a node operator with a fraction of the stake $x$, employing an inclusion strategy which cuts profits to a fraction $y$ of the max MEV, and say this max has an expected value $M$.
This node operator will have an expected profit per block of $Mx^2y + Mx(1-x) = Mx(1 - x(1-y))$, which corresponds a loss of a fraction $x(1-y)$ of the theoretical maximum $Mx$. This makes sense, as $1-y$ is the fraction of profits which is on average missed by their own sub-optimal proposals, which are a fraction $x$ of all proposals. Even if we gave proposers full control over inclusion, at worst an operator can decide to never include any transaction, which reduces global profits to $M(1-x)$, and the operator's profits to $M(1-x)x$, i.e. a node operator is only responsible for a percentage of their profits which is equal to their stake, and that's the most that their altruism can cost them.
Of course if everyone is altruistic then everyone's profits can be substantially reduced, but crucially we move from a world in which an individual decision to be altruistic carries a heavy penalty to one in which this penalty is shared by everyone, and moreover in which the cost of altruism is proportional one's stake. If we are content with 10% of proposals being mindful of censorship and actively resisting it, all we need is that 10% of the stake is made of weakly-altruistic solo-validators, whose individual decisions to resist censorships are essentially irrelevant to their own profits. Even globally, the cost is at most a 10% reduction in profits, and in reality it will be much less, since being mindful of censorship does not require giving up all profits, or even most: all MEV extraction which does not require censorship can go on unimpeded, because builders have a large portion of the block to work with. Most importantly, regardless of who the altruistic actors are, the cost of censorship resistance is now evenly spread out over the whole validator set, and it can become sustainable for everyone!
[^bignote1]: This is not exactly right, because profits are shared within committees and not globally, so a single sub-optimal block does not equally penalize everyone, but rather only the members of the committee. Nonetheless, for any sufficiently large concentration of stake the effect is the same, i.e. missed profits because of other validators' sub-optimal strategies are proportional to stake. Moreover, if a sufficiently large percentage of the stake follows some similar censorship-resistant inclusion strategy, the missed profits caused by this strategy become quickly proportional to stake for everyone. For example, say 10% of validators follow the same strategy, so 10% of blocks are similarly sub-optimal. Within a short period of time, all validators will converge to having been committee members of sub-optimal blocks for 10% of their assigned blocks, and thus each individual validator will have the same missed profits.
### The new economics of censorship resistance
Let's try to further analyze these improvements and figure out how much more censorship resistance they can buy us. In the plain builders/proposer scheme every operator incurs the same cost per validator that they decide to use for censorship resistance (or other sub-optimal inclusion strategies), no matter how many they control. As we discussed, this changes with MEV smoothing, making the cost proportional to stake.
Suppose each operator has their own evaluation of the marginal utility curve of censorship resistance, meaning they can evaluate how much they are willing to pay for an extra "unit" of censorship resistance, or in other words how much of their profits they are willing to give up for it. With MEV smoothing, an operator with a fraction $p$ of the stake incurs a cost that is a fraction $p$ of what they would have incurred in the plain builders/proposer scheme, while providing the same contribution to censorship resistance. Effectively, they are able to invest up to $\frac{1}{p}$ more into censorship resistance (potentially less, limited by the maximum amount that their validators are able to provide) than they did before, because the cost of the investment is shared across the validator set
For example, suppose that optimal censorship-resistant strategy for a single validator reduces their profits by 50%. One specific solo validator decides that the maximum they are willing to give up is 5% of their profits. In the plain builders/proposer scheme, they therefore decide to implement this strategy only for 10% of the blocks they propose, providing only 10% of their maximum capacity for censorship-resistance. On the other end, with MEV smoothing implementing it for all blocks they propose costs them only 0.00025% of their profits, and so they decide to do so, maxing out their censorship-resistance capacity.
Even considering the theoretical maximum 0.0005% of missed profits, it is clear that it is such a negligible amount that any even remotely long-term aligned solo validator would be incentivized to provide the maximum amount of censorship resistance they can. For an operator controlling 100 validators, the theoretical maximum of missed profits would be 0.05%, still quite small, and a more realistic estimation of the costs of a censorship-free inclusion strategy would likely reduce this cost by an order of magnitude, because it certainly wouldn't entail giving up a majority of MEV. Therefore, we can expect operators controlling maybe even up to a 1000 validators to be willing to provide as much censorship resistance as it is needed from them, and the sum of their contributions should be plenty of censorship resistance as long as the stake stays sufficiently decentralized!
## Changing the fork-choice rule to allow MEV smoothing without latency constraints
_Thanks to [Caspar](https://twitter.com/casparschwa) for writing a large part of this section and for useful discussions_
We are trying to solve the same problems which the (block, slot) approach solves, but *without* introducing latency constraints. We can do so by changing the way attestations give weight to blocks. In short, the new fork choice rule can count attestations for the *same* block differently.
Attestations in slot $n$ not only vote for a source, target and head, but also attach their local view of the max-value $p_{i,n}$. This helps because blocks publish a payment value $p_{n}$ (to be shared across committee and proposer), and so we can compare the attestation's $p_{i,n}$ value to the block's $p_n$ value.
Consider the following scenario. At slot $n$ there is a block `A`. At slot $n+1$ block `B` is published with payment $p_{n+1}$. Then committee members of slot $n+1$ will start attesting, e.g. validator $i$ attests with $i$'s local view of the max-value $p_{i, n+1}$ of slot $n+1$.
This allows us to check whether $p_{i, n+1}$ was smaller, equal or greater than the offered payment $p_{n+1}$:
- $p_{i, n+1} > p_{n+1}$ > : add no weight, "not good enough".
- $p_{i, n+1} \leq p_{n+1}$: add weight, "good enough or even better than what I have heard so far".
If a majority of committee members attest with local $p_i$-values below or equal to the offered payment $p$ by the block, it should in normal circumstances end up being canonical.
Will an honest, but late block `B` become canonical? Yes! Let's consider the scenario where block `B` is late:
- Honest committee members will attest to block `A` posting $p_{i, n+1}$
- If block `B` for whatever reason arrives late, the fork choice can differentiate between giving block `B` weight or not by comparing the $p_i$ values to the $p$ value:
- If $p_{n+1} >= p_{i, n+1}$ block `B` should inherit weight
- If $p_{i, n+1} > p_{n+1}$ block `B` should not inherit weight
There's unfortunately a problem with this solution. Say block `B` is late, so block `C` builds on block `A`. How does the weight inheritance work for block `C`?
- If `C` inherits all weight, then you can just deliberately fork out block `B`, even if it is a good block (assuming that one attestation doesn't consider block `B` good)
- If you only pass on weight to `C` in which attestations consider `B` to be non-maximal, i.e. "not good", then `C` gets punished even though it's not `C`'s fault that block `B` was late... `B` could be considered good by all attestations, then `C` immediately has no chance...
#### Proposed fix
We can use a majority criterion to determine how attestations count, rather than just looking at their individual p-values. *Crucially, we need to do this in a way that C is not disadvantaged when B is late, but it is also not able to fork out B at will.*
Definitions:
- $a_s$ (s for sum) is the cumulative weight on A up to slot $n$
- $a_1$ is the weight of attestations to A at slot n+1, whose payment is $\leq$ to that of B (i.e. these support the maximality claim of B)
- $a_2$ is the weight of attestations to A at slot n+1, whose payment is $>$ to that of B (i.e. these don't support the maximality claim of B)
- $b$ is weight of direct attestations to B
Weight inheritance can work in the following way, given the usual setup of A,B,C with B and C built on A in consecutive slots:
- A has weight $a_s + a_1 + a_2$, and C inherits all of it
- If $a_1 + b \geq a_2$ (i.e. a majority supports the maximality claim of B $b$), then B gets weight $a_s + a_1 + a_2 + b$, so it also inherits all attestations to A
- If $a_2 > a_1 + b$, then B gets weight $a_s + a_1 + b$, i.e. it only gets the weight of attestations supporting its maximality.
Generally speaking, the idea is that everything works as it would normally, except if a majority thinks B is bad, in which case only the minority of attestations which think B is good count for it. Assuming an honest majority of informed attesters whose votes are not too delayed, this is what this entails:
- good B: $a_1 + b \geq a_2$, so B inherits the full weight of A. If C forks from A, it also inherits the weight of A, but B might win if $b > 0$. As we said, when B is good everything works as it does now.
- bad B: $a_2 > a_1 + b$. Both C and B get $a_1$, but only C gets $a_2$ and only B gets $b$. Overall, C gets $a_2 - b > 0$ more weight than B
Case in which a majority thinks B is bad. This is about inheritance of attestations, not blocks, so the upper branch accumulates attestations to B and the lower one to C:
```graphviz
digraph hierarchy {
nodesep=1.0 // increases the separation between nodes
rankdir=RL //
node [color=black,fontname=Courier,shape=circle, width=1] //
edge [color=black, style=solid] //
"a1+a2"->a_s
a1->a_s
b->a1
c->"a1+a2"
}
```
Case in which a majority thinks B is good:
```graphviz
digraph hierarchy {
nodesep=1.0 // increases the separation between nodes
rankdir=RL //
node [color=black,fontname=Courier,shape=circle, width=1] //
edge [color=black, style=solid] //
"a1+a2"->a_s
b->"a1+a2"
c->"a1+a2"
}
```
#### Concerns:
Long reorgs are not possible, because the difference between the good and bad scenarios is only the weight which B inherits, and in particular the difference in inherited weights between the two is exactly $a_2$, so bounded by the committee weight $w_c$ for slot $n+1$. Moreover, you'd expect a switch from one scenario to the other in situations in which $a_1 + b$ and $a_2$ are close, in which case $a_2$ should be roughly bounded by $w_c/2$.
Nonetheless, we don't want to create an easier way to do one or two block reorgs... What are the risks?
- A majority thinks the block is good, but initially a majority of visible attestations says otherwise. C builds on A, but more attestations come out and the majority is flipped. Now attestations to A support B and C equally, but B can also have some of its own attestations, and beat C.
- A majority thinks the block is bad, but initially a majority of visible attestations says otherwise. C builds on B, but more attestations come out and the majority is flipped. Now A has extra weight $a_2 - b > 0$ compared to B, so it beats C (assuming C has not gotten any attestations in the meantime)
If we were to update attestation counts in a local view only at the end of the slot (say up to 10s), which lets the next proposer operate on a "stable view", would this problem mostly go away? (besides when there's really bad network conditions, in which case some forking should be ok as long as it doesn't force empty blocks)
Under normal conditions, C's proposer should have time to figure out which attestations will apply over the next slot, including which side will have the majority, and thus it should be able to correctly choose whether to build on A or B.
Also under normal conditions, a correct choice by C should be attested to by most of its committee, which should overpower any change induced by a majority shift in the previous slot, since it can in the best case induce a weight change of $w_c$, but really it should be much much less, so a further block built on C should be very unlikely to be reorged out because of such a shift.
In principle, shifts should not happen at all under normal conditions, because the count of $p$ values for or against B should be very one-sided.
## Other aspects
### Greedy maximization is not the only strategy
Over a sufficiently long period of time, MEV is greater when many blocks are subject to some centralized control, which allows for reliable services to be offered. For example, running an MEV relayer with 10% of hashrate using it is very different from doing so with 80% of hashrate, which is why [Eden Network](https://edennetwork.io/) is trying to use token issuance to essentially buy control of the priority space of more blocks. Even if builder/proposer separation were implemented, something like Eden Network could still function the way it does now, using long-term priority space auctions to create more predictable rewards and potentially even more rewards overall, because predictable access to priority space might command a premium, from bots, wallets or protocols alike.
In general, many proposers might have reasons to prefer MEV maximization strategies other than choosing the highest paying block from the builders' market, which is essentially greedy maximization. This might be especially the case for exchanges, for which integrating proposing powers in their business might create very different long-term incentives than for solo validators. For example, an exchange might find more value in a block with nominally less MEV extracted, but which allows them to quickly insert their customers' transactions, and so they might prefer to forgo the block content market and make their own blocks. On the other end, this committee-based smoothing scheme forces all proposers to adapt to the builders' market at least in their payments, which have to conform to greedy maximization. If someone wants to adopt a different strategy which is overall more profitable, they need to share some of the profits with everyone else.
### MEV income distribution for pooled stake
MEV income distribution for staking pools and SSV solutions should be much easier with MEV smoothing. A priori, agreements can be made on how this distribution is supposed to be conducted, i.e. deciding the split between stakers and pool, or a leader-based SSV will split MEV among all the shared validators. The question then becomes, how do we verify that the distribution is done as agreed?
The reason why this is problematic is that detection of MEV is not easy at all, and attribution is even harder: good luck trying to tell how much money a pool actually made on a block. Even with the builders/proposer separation scheme, the payment accepted by the proposer is not reliable in this sense: a block builder could bribe a pool to have them accept blocks with sub-optimal payments (which are the part that stakers can easily request a share of, even directly on-chain), effectively funneling MEV away from the stakers and to the pool.
With this scheme, and given a minimum of competition in the block content market, such deals should not be possible, because maximality is enforced (and all builders have an incentive to make sure that their block reaches everyone, if they produce a good one), so the amount of payments which are funneled away from the transparent payment mechanism should be minimal. Basically the accepted payments should work as a somewhat reliable MEV oracle. Distribution of rewards can then be even entirely on-chain, without the need to have any complex monitoring system. Besides, if you really wanted to build a monitoring system that works, what you’d do is probably try to get a good view of the block content market and use that as a proxy for MEV. Now this view is accessible on-chain, and the builders are incentivized to make it reliable.

